
分析 (1)利用等差数列的通项公式及其前n项和公式即可得出;
(2)由于$\frac{S_n}{n}=\frac{n-5}{2}$,利用等差数列的通项公式及其前n项和公式可得Tn,再利用二次函数的单调性即可得出.
解答 解:(1)∵{an}为等差数列,首项为a1,公差设为d,
则依题意有$\left\{\begin{array}{l}({a_1}+d)+({a_1}+4d)=1\\ 15{a_1}+\frac{15×14}{2}d=75\end{array}\right.$,
解得$\left\{\begin{array}{l}{a_1}=-2\\ d=1\end{array}\right.$,
∴${S_n}={a_1}n+\frac{n(n-1)}{2}d=-2n+\frac{n(n-1)}{2}=\frac{{{n^2}-5n}}{2}$.
(2)∵${S_n}=\frac{{{n^2}-5n}}{2}$,∴$\frac{S_n}{n}=\frac{n-5}{2}$.
设${b_n}=\frac{S_n}{n}=\frac{n-5}{2}$,则${b_{n+1}}-{b_n}=\frac{(n+1)-5}{2}-\frac{n-5}{2}=\frac{1}{2}$,
∴数列{bn}是公差为$\frac{1}{2}$的等差数列,首项为${b_1}=\frac{S_1}{1}={a_1}=-2$,
Tn为数列$\left\{{\frac{S_n}{n}}\right\}$的前n项和,
∴${T_n}=-2n+\frac{n(n-1)}{2}•\frac{1}{2}=\frac{{{n^2}-9n}}{4}$.
又∵$y=\frac{{{x^2}-9x}}{4}$图象开口向上,对称轴为$x=\frac{9}{2}$,且n∈N*,
∴n=4或n=5时,${({T_n})_{min}}=\frac{{{4^2}-9×4}}{4}=-5$.
点评 本题考查了等差数列的通项公式及其前n项和公式、二次函数的单调性,考查了推理能力与计算能力,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
| 甲 | 80 | 110 | 120 | 140 | 150 |
| 乙 | 100 | 120 | x | 100 | 160 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{4}$ | B. | $\frac{3}{4}$π | C. | $\frac{π}{4}$或$\frac{3}{4}$π | D. | $\frac{π}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
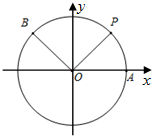 如图,A是单位圆与x轴正半轴的交点,点P、B在单位圆上,设∠AOP=θ,∠AOB=α,且$\overrightarrow{OQ}$=$\overrightarrow{OA}$+$\overrightarrow{OP}$.
如图,A是单位圆与x轴正半轴的交点,点P、B在单位圆上,设∠AOP=θ,∠AOB=α,且$\overrightarrow{OQ}$=$\overrightarrow{OA}$+$\overrightarrow{OP}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{60}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{59}{60}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com