
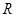 上的函数
上的函数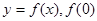
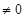 ,当
,当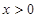 时,
时,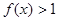 ,且对任意的
,且对任意的 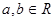 ,有
,有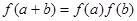 ,
,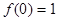 ;
;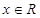 ,恒有
,恒有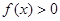 ;
;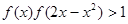 ,求
,求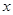 的取值范围.
的取值范围.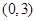 .
.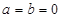 即可得证;(Ⅱ)令
即可得证;(Ⅱ)令 得,
得,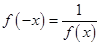 ,由已知x>0时,f(x)>1>0,当x<0时,-x>0,f(-x)>0,故对任意x∈R,f(x)>0;(Ⅲ)先证明
,由已知x>0时,f(x)>1>0,当x<0时,-x>0,f(-x)>0,故对任意x∈R,f(x)>0;(Ⅲ)先证明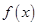 为增函数:任取x2>x1,则
为增函数:任取x2>x1,则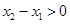 ,
,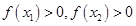 ,故
,故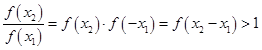 ,故其为增函数;然后利用单调性脱
,故其为增函数;然后利用单调性脱 解一元二次不等式.
解一元二次不等式.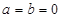 ,则f(0)=[f(0)]2 ∵ f(0)≠0 ∴ f(0)=1 2分
,则f(0)=[f(0)]2 ∵ f(0)≠0 ∴ f(0)=1 2分 则 f(0)=f(x)f(-x)∴
则 f(0)=f(x)f(-x)∴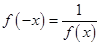 4分
4分 ,又x=0时,f(0)=1>0 6分
,又x=0时,f(0)=1>0 6分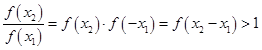


湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com