
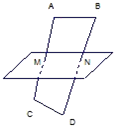
 如图,AB、CD都平行于平面α,AB=5,CD=3,AC,BD与α分别交于M,N两点,M为的AC中点,则MN长的取值范围是________.
如图,AB、CD都平行于平面α,AB=5,CD=3,AC,BD与α分别交于M,N两点,M为的AC中点,则MN长的取值范围是________.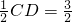 ,PN=
,PN=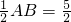 ,在三角形MNP中利用两边之和大于第三边,得则MN长的取值范围是(0,4],问题得到解答.
,在三角形MNP中利用两边之和大于第三边,得则MN长的取值范围是(0,4],问题得到解答.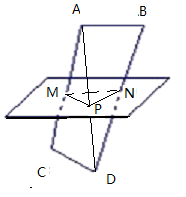 解:连接AD,取AD中点P,再连接NP、MP、MN,
解:连接AD,取AD中点P,再连接NP、MP、MN,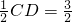 ,PN=
,PN=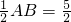 ,
,

科目:高中数学 来源: 题型:

查看答案和解析>>
科目:高中数学 来源: 题型:
如图,在几何体ABCDE中,△ABC是等腰直角三角形,![]() ,BE和CD都垂直于平面ABC,且BE=AB=2,CD=1,点F是AE的中点。
,BE和CD都垂直于平面ABC,且BE=AB=2,CD=1,点F是AE的中点。

(1)证明:DF∥平面ABC;
(2)求AB与平BDF所成角的大小。
查看答案和解析>>
科目:高中数学 来源:2012-2013学年广东省汕尾市陆丰市新龙中学高一(上)第二次月考数学试卷(解析版) 题型:解答题

查看答案和解析>>
科目:高中数学 来源:2012-2013学年广东省汕尾市陆丰市新龙中学高一(上)第二次月考数学试卷(解析版) 题型:解答题

查看答案和解析>>
科目:高中数学 来源:2006-2007学年广东省广州89中学高一(上)期末数学复习试卷(必修1、2)(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com