
分析 通过分n=2k-1、n=2k两种情况分组求和可知Sn的表达式,进而计算可得结论.
解答 解:依题意,当n=2k-1时,
Sn=S2k-1
=1-2+3-4+…+[-(2k-1)]2k-1-1
=2k-1-k
=k-1;
当n=2k时,
Sn=S2k
=1-2+3-4+…+[-(2k)]2k-1
=-k;
综上所述,Sn=$\left\{\begin{array}{l}{\frac{n+1}{2},}&{n为奇数}\\{-\frac{n}{2},}&{n为偶数}\end{array}\right.$,
∴S17+S33+S50=$\frac{17+1}{2}$+$\frac{33+1}{2}$-$\frac{50}{2}$
=$\frac{18+34-50}{2}$
=1,
故答案为:1.
点评 本题考查数列的通项及前n项和,考查分类讨论的思想,注意解题方法的积累,属于中档题.


 全优点练单元计划系列答案
全优点练单元计划系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
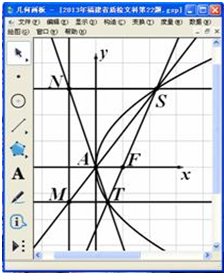 某同学用《几何画板》研究抛物线的性质:打开《几何画板》软件,绘制某抛物线E:y2=2px,在抛物线上任意画一个点S,度量点S的坐标(xS,yS),如图.
某同学用《几何画板》研究抛物线的性质:打开《几何画板》软件,绘制某抛物线E:y2=2px,在抛物线上任意画一个点S,度量点S的坐标(xS,yS),如图.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com