
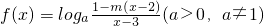 ,
,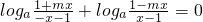 〔〕
〔〕
 x∈(b,a)的值域为(0,a),〔〕
x∈(b,a)的值域为(0,a),〔〕 在x∈(b,a)上是减函数,所以
在x∈(b,a)上是减函数,所以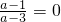 ,这是不可能的.〔〕
,这是不可能的.〔〕 x∈(b,a)的值域为(a,+∞),〔〕
x∈(b,a)的值域为(a,+∞),〔〕 在x∈(b,a)上是减函数,并且b=3〔〕
在x∈(b,a)上是减函数,并且b=3〔〕 ,解得
,解得 〔〕
〔〕 ,b=3〔〕
,b=3〔〕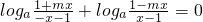 化简得:(m2-1)x2=0对定义域内的任意x成立,即可求得m 值;
化简得:(m2-1)x2=0对定义域内的任意x成立,即可求得m 值; ,由f(x)的取值范围恰为(1,+∞),对a进行分类讨论:当0<a<1时,当a>1时,分别求得实数a,b的值即可.
,由f(x)的取值范围恰为(1,+∞),对a进行分类讨论:当0<a<1时,当a>1时,分别求得实数a,b的值即可.

 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:2012-2013学年上海外国语大学附中高三(上)第一次周练数学试卷(解析版) 题型:解答题
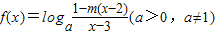 ,
,查看答案和解析>>
科目:高中数学 来源:2010-2011学年江苏省宿迁市泗阳中学高一(下)月考数学试卷(解析版) 题型:解答题
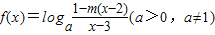 ,
,查看答案和解析>>
科目:高中数学 来源:2006年广州市普通高中11月学业水平测试数学试卷(解析版) 题型:选择题
 ,对定义域内的任意x都有f(2-x)+f(2+x)=0成立.则实数m的值为( )
,对定义域内的任意x都有f(2-x)+f(2+x)=0成立.则实数m的值为( )查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com