
【题目】
甲、乙、丙三名射击运动员射中目标的概率分别为![]()
![]() ,三人各射击一次,击中目标的次数记为
,三人各射击一次,击中目标的次数记为![]() .
.
(1)求![]() 的分布列及数学期望;
的分布列及数学期望;
(2)在概率![]() (
(![]() =0,1,2,3)中, 若
=0,1,2,3)中, 若![]() 的值最大, 求实数
的值最大, 求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() ,ξ的分布列为
,ξ的分布列为
ξ | 0 | 1 | 2 | 3 |
P |
|
|
|
|
(2)![]()
【解析】
(1)P(ξ)是“ξ个人命中,3-ξ个人未命中”的概率.其中ξ的可能取值为0、1、2、3.
P(ξ=0)=![]()
![]()
![]() (1-a)2=
(1-a)2=![]() (1-a)2;
(1-a)2;
P(ξ=1)=![]() ·
·![]()
![]() (1-a)2+
(1-a)2+![]()
![]()
![]() a(1-a)=
a(1-a)=![]() (1-a2);
(1-a2);
P(ξ=2)=![]() ·
·![]()
![]() a(1-a)+
a(1-a)+![]()
![]()
![]() a2=
a2=![]() (2a-a2);
(2a-a2);
P(ξ=3)=![]() ·
·![]()
![]() a2=
a2=![]() .
.
所以ξ的分布列为
ξ | 0 | 1 | 2 | 3 |
P |
|
|
|
|
ξ的数学期望为
E(ξ)=0×![]() (1-a)2+1×
(1-a)2+1×![]() (1-a2)+2×
(1-a2)+2×![]() (2a-a2)+3×
(2a-a2)+3×![]() =
=![]() .
.
(2)P(ξ=1)-P(ξ=0)=![]() [(1-a2)-(1-a)2]=a(1-a);
[(1-a2)-(1-a)2]=a(1-a);
P(ξ=1)-P(ξ=2)=![]() [(1-a2)-(2a-a2)]=
[(1-a2)-(2a-a2)]=![]() ;
;
P(ξ=1)-P(ξ=3)=![]() [(1-a2)-a2]=
[(1-a2)-a2]=![]() .
.
由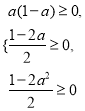 和0<a<1,得0<a≤
和0<a<1,得0<a≤![]() ,即a的取值范围是
,即a的取值范围是![]() .
.


 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案科目:高中数学 来源: 题型:
【题目】关于函数![]() 有下列四个结论:
有下列四个结论:
①![]() 是偶函数;②
是偶函数;②![]() 的最小正周期为
的最小正周期为![]() ;③
;③![]() 在
在![]() 上单调递增;④
上单调递增;④![]() 的值域为
的值域为![]() .
.
上述结论中,正确的为( )
A.③④B.②④C.①③D.①④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某园林单位准备绿化一块直径为BC的半圆形空地,△ABC外的地方种草,△ABC的内接正方形PQRS为一水池,其余的地方种花.若BC=a,∠ABC=![]() ,设△ABC的面积为S1,正方形的面积为S2.
,设△ABC的面积为S1,正方形的面积为S2.
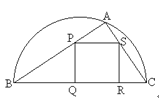
(1)用a,![]() 表示S1和S2;
表示S1和S2;
(2)当a固定,![]() 变化时,求
变化时,求![]() 取最小值时的角
取最小值时的角![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】根据幼儿身心发展的特征,幼儿园通常着重在健康、科学、社会、语言、艺术五大领域对幼儿展开全方位的教育和培养.经调查发现,一个幼儿除了在幼儿园进行五大领域的系统学习之外,还会报一些课外兴趣班.而家长朋友们对于是否额外报这些课外兴趣班的态度也是不一样的.某调查机构对某幼儿园的100名幼儿家长就孩子是否报课外兴趣班的赞同程度进行调查统计,得到家长对幼儿报课外兴趣班赞同度![]() 的频数分布表:
的频数分布表:
赞同度 |
|
|
|
|
|
家长数 | 2 | 12 | 14 | 28 | 44 |
(1)分别计算对幼儿报兴趣班的赞同度不低于![]() 的家长比例和对幼儿报兴趣班的赞同度低于
的家长比例和对幼儿报兴趣班的赞同度低于![]() 的家长比例;
的家长比例;
(2)求家长对幼儿报兴趣班的赞同度的平均数与方差的估计值.(同一组中的数据用该组区间的中点值代替)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() 为抛物线
为抛物线![]() 的焦点,过点
的焦点,过点![]() 任作两条互相垂直的直线
任作两条互相垂直的直线![]() ,
,![]() ,分别交抛物线
,分别交抛物线![]() 于
于![]() ,
,![]() ,
,![]() ,
,![]() 四点,
四点,![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点.
的中点.
(1)求证:直线![]() 过定点,并求出该定点的坐标;
过定点,并求出该定点的坐标;
(2)设直线![]() 交抛物线
交抛物线![]() 于
于![]() ,
,![]() 两点,试求
两点,试求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】陕西关中的秦腔表演朴实,粗犷,细腻,深刻,再有电子布景的独有特效,深得观众喜爱.戏曲相关部门特意进行了“喜爱看秦腔”调查,发现年龄段与爱看秦腔的人数比存在较好的线性相关关系,年龄在![]() ,
,![]() ,
,![]() ,
,![]() 的爱看人数比分别是0.10,0.18,0.20,0.30.现用各年龄段的中间值代表年龄段,如42代表
的爱看人数比分别是0.10,0.18,0.20,0.30.现用各年龄段的中间值代表年龄段,如42代表![]() .由此求得爱看人数比
.由此求得爱看人数比![]() 关于年龄段
关于年龄段![]() 的线性回归方程为
的线性回归方程为![]() .那么,年龄在
.那么,年龄在![]() 的爱看人数比为( )
的爱看人数比为( )
A.0.42B.0.39C.0.37D.0.35
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com