
【题目】已知椭圆C方程:![]() +
+![]() =1(a>b>0),M(x0 , y0)是椭圆C上任意一点,F(c,0)是椭圆的右焦点.
=1(a>b>0),M(x0 , y0)是椭圆C上任意一点,F(c,0)是椭圆的右焦点.
(1)若椭圆的离心率为e,证明|MF|=a﹣ex0;
(2)已知不过焦点F的直线l与圆x2+y2=b2相切于点Q,并与椭圆C交于A,B两点,且A,B两点都在y轴的右侧,若a=2,求△ABF的周长.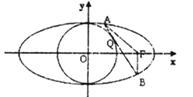
【答案】证明:(1)∵M(x0 , y0)是椭圆C上任意一点,椭圆的右准线方程为x=![]() ,
,
∴![]() =e
=e
∴|MF|=a﹣ex0;
(2)解:设A(x1 , y1),B(x2 , y2).(x1>0,x2>0),
连接OA,OQ,在△OAQ中,|AQ|2=x12+y12﹣b2 ,
∵y12=b2﹣![]() x12 ,
x12 ,
∴|AQ|2=1﹣![]() x12=e2x12;
x12=e2x12;
∴|AQ|=ex1 ,
同理:|BQ|=ex2 ,
∴|AB|=|AQ|+|BQ|=e(x1+x2)
∴|AB|+|AF|+|BF|=e(x1+x2)+a﹣ex1+a﹣ex2=2a
∴a=2时,△ABF的周长为4.
【解析】(1)利用椭圆的第二定义,即可得出结论;
(2)证明|AQ|=ex1 , |BQ|=ex2 , 即可求出△ABF的周长.


科目:高中数学 来源: 题型:
【题目】设函数![]() ,
,![]() .
.
(1)![]() 在
在![]() 处的切线方程;
处的切线方程;
(2)当![]() 时,函数
时,函数![]() 有两个极值点,求
有两个极值点,求![]() 的取值范围;
的取值范围;
(3)若![]() 在点
在点![]() 处的切线与
处的切线与![]() 轴平行,且函数
轴平行,且函数![]() 在
在![]() 时,其图象上每一点处切线的倾斜角均为锐角,求
时,其图象上每一点处切线的倾斜角均为锐角,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数列![]() 的前
的前![]() 项和为
项和为![]() ,若数列
,若数列![]() 的各项按如下规律排列:
的各项按如下规律排列:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,…,
,…,![]() ,
,![]() , …,
, …,![]() ,…有如下运算和结论:①
,…有如下运算和结论:①![]() ;②数列
;②数列![]() ,
,![]() ,
,![]() ,
,![]() ,…是等比数列;③数列
,…是等比数列;③数列![]() ,
,![]() ,
,![]() ,
,![]() ,…的前
,…的前![]() 项和为
项和为![]() ;④若存在正整数
;④若存在正整数![]() ,使
,使![]() ,
,![]() ,则
,则![]() .其中正确的结论是_____.(将你认为正确的结论序号都填上)
.其中正确的结论是_____.(将你认为正确的结论序号都填上)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(1)设直线![]() 的方程为
的方程为![]() .若直线
.若直线![]() 在两坐标轴上的截距相等,求直线
在两坐标轴上的截距相等,求直线![]() 的方程;
的方程;
(2)过直线![]() :
:![]() 上的点
上的点![]() 作直线
作直线![]() ,若直线
,若直线![]() ,
,![]() 与
与![]() 轴围成的三角形的面积为2,则直线
轴围成的三角形的面积为2,则直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了弘扬民族文化,某中学举行了“我爱国学,传诵经典”考试,并从中随机抽取了60名学生的成绩(满分100分)作为样本,其中成绩不低于80分的学生被评为优秀生,得到成绩分布的频率分布直方图如图所示.

(1)若该所中学共有2000名学生,试利用样本估计全校这次考试中优秀生人数;
(2)(i)试估计这次参加考试的学生的平均成绩(同一组数据用该组区间的中点值作代表);
(ii)若在样本中,利用分层抽样的方法从成绩不低于70分的学生中随机抽取6人,再从中抽取3人赠送一套国学经典学籍,试求恰好抽中2名优秀生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=3,BC=2,点M,N分别是边AB,CD上的点,且MN∥BC,![]()
![]() .若将矩形ABCD沿MN折起使其形成60°的二面角(如图).
.若将矩形ABCD沿MN折起使其形成60°的二面角(如图).

(1)求证:平面CND⊥平面AMND;
(2)求直线MC与平面AMND所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 的三个顶点
的三个顶点![]() ,其外接圆为圆
,其外接圆为圆![]() .
.
(1)若直线![]() 过点
过点![]() ,且被圆
,且被圆![]() 截得的弦长为
截得的弦长为![]() ,求直线
,求直线![]() 的方程;
的方程;
(2)对于线段![]() (包括端点)上的任意一点
(包括端点)上的任意一点![]() ,若在以
,若在以![]() 为圆心的圆上都存在不同的两点
为圆心的圆上都存在不同的两点![]() ,使得点
,使得点![]() 是线段
是线段![]() 的中点,求圆
的中点,求圆![]() 的半径
的半径![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某市高三教学质量检测中,全市共有![]() 名学生参加了本次考试,其中示范性高中参加考试学生人数为
名学生参加了本次考试,其中示范性高中参加考试学生人数为![]() 人,非示范性高中参加考试学生人数为
人,非示范性高中参加考试学生人数为![]() 人.现从所有参加考试的学生中随机抽取
人.现从所有参加考试的学生中随机抽取![]() 人,作检测成绩数据分析.
人,作检测成绩数据分析.

(1)设计合理的抽样方案(说明抽样方法和样本构成即可);
(2)依据![]() 人的数学成绩绘制了如图所示的频率分布直方图,据此估计本次检测全市学生数学成绩的平均分;
人的数学成绩绘制了如图所示的频率分布直方图,据此估计本次检测全市学生数学成绩的平均分;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com