
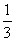 (m∈R,e=2.718 28…是自然对数的底数).
(m∈R,e=2.718 28…是自然对数的底数).(1)求函数f(x)的极值;
(2)当x>0时,设f(x)的反函数为f-1(x),对0<p<q,试比较f(q-p)、f-1(q-p)及f-1(q)-f-1(p)的大小.
(文)已知函数f(x)=x3+bx2+cx+d(b、c、d∈R且都为常数)的导函数为f′(x)=3x2+4x,且f(1)=7,设F(x)=f(x)-ax2(a∈R).
(1)当a<2时,求F(x)的极小值;
(2)若对任意的x∈[0,+∞),都有F(x)≥0成立,求a的取值范围并证明不等式a2-13a+39≥![]() .
.
答案:(理)解:(1)∵当x>0时,f(x)=ex-1在(0,+∞)上单调递增,且f(x)=ex-1>0;
当x≤0时,f(x)=![]() x3+mx2,此时f′(x)=x2+2mx=x(x+2m).
x3+mx2,此时f′(x)=x2+2mx=x(x+2m).
①若m=0时,f′(x)=x2≥0,则f(x)=![]() x3在(-∞,0]上单调递增,且f(x)=
x3在(-∞,0]上单调递增,且f(x)=![]() x3≤0.又f(0)=0,可知函数f(x)在R上单调递增,无极值.
x3≤0.又f(0)=0,可知函数f(x)在R上单调递增,无极值.
②若m<0,令f′(x)=x(x+2m)>0![]() x<0或x>-2m(舍去).函数f(x)=
x<0或x>-2m(舍去).函数f(x)=![]() x3+mx2在(-∞,0]上单调递增,同理,函数f(x)在R上单调递增,无极值.
x3+mx2在(-∞,0]上单调递增,同理,函数f(x)在R上单调递增,无极值.
③若m>0,令f′(x)=x(x+2m)>0![]() x>0或x<-2m.函数f(x)=
x>0或x<-2m.函数f(x)=![]() x3+mx2在(-∞,-2m]上单调递增,在(-2m,0]上单调递减.此时函数f(x)在x=-2m处取得极大值:f(-2m)=
x3+mx2在(-∞,-2m]上单调递增,在(-2m,0]上单调递减.此时函数f(x)在x=-2m处取得极大值:f(-2m)=![]() m3+4m3=
m3+4m3=![]() m3>0;又f(x)在(0,+∞)上单调递增,故在x=0处取得极小值:f(0)=0.综上可知,当m>0时,f(x)的极大值为
m3>0;又f(x)在(0,+∞)上单调递增,故在x=0处取得极小值:f(0)=0.综上可知,当m>0时,f(x)的极大值为![]() m3,极小值为0;当m≤0时,f(x)无极值.
m3,极小值为0;当m≤0时,f(x)无极值.
(2)当x>0时,设y=f(x)=ex-1![]() y+1=ex
y+1=ex![]() x=ln(y+1).∴f-1(x)=ln(x+1)(x>0).①比较f(q-p)与f-1(q-p)的大小.记g(x)=f(x)-f-1(x)=ex-ln(x+1)-1(x>0).∵g′(x)=ex-
x=ln(y+1).∴f-1(x)=ln(x+1)(x>0).①比较f(q-p)与f-1(q-p)的大小.记g(x)=f(x)-f-1(x)=ex-ln(x+1)-1(x>0).∵g′(x)=ex-![]() 在(0,+∞)上是单调递增函数,∴g′(x)>g′(0)=e0-
在(0,+∞)上是单调递增函数,∴g′(x)>g′(0)=e0-![]() =0恒成立.∴函数g(x)在(0,+∞)上单调递增.∴g(x)>g(0)=e0-ln(0+1)-1=0.当0<p<q时,有q-p>0,∴g(q-p)=eq-p-ln(q-p+1)-1>0.∴eq-p-1>ln(q-p+1),
=0恒成立.∴函数g(x)在(0,+∞)上单调递增.∴g(x)>g(0)=e0-ln(0+1)-1=0.当0<p<q时,有q-p>0,∴g(q-p)=eq-p-ln(q-p+1)-1>0.∴eq-p-1>ln(q-p+1),
即f(q-p)>f-1(q-p).①9分
②比较f-1(q-p)与f-1(q)-f-1(p)的大小.ln(q-p+1)-[ln(q+1)-ln(p+1)]=ln(q-p+1)-ln(q+1)+ln(p+1)
=ln![]() =ln
=ln![]()
=ln![]() =ln[
=ln[![]() +1].
+1].
∵0<p<q,∴![]() +1>1,故ln[
+1>1,故ln[![]() +1]>0.∴ln(q-p+1)>ln(q+1)-ln(p+1),
+1]>0.∴ln(q-p+1)>ln(q+1)-ln(p+1),
即f-1(q-p)>f-1(q)-f-1(p).②
(注:也可用分析法或考查函数h(x)=ln(x-p+1)-ln(x+1)+ln(p+1),x∈(p,+∞).
求导可知h(x)在(p,+∞)上单调递增.∴h(x)>h(p)恒成立,而h(p)=0.∴h(x)>0在x∈(p,+∞)上恒成立.∵q∈(p,+∞),∴h(q)>0恒成立)∴由①②可知,当0<p<q时,有f(q-p)>f-1(q-p)>f-1(q)-f-1(p).12分
(文)解:(1)∵f′(x)=3x2+4x=3x2+2bx+c,∴b=2,c=0.∴f(x)=x3+2x2+d.
又∵f(1)=7,∴d=4.∴f(x)=x3+2x2+4.2分
∴F(x)=f(x)-ax2=x3+2x2+4-ax2=x3+(2-a)x2+4.则F′(x)=3x2+2(2-a)x.
由F′(x)=0求得x1=![]() ,x2=0.∵a<2,∴x1<x2.
,x2=0.∵a<2,∴x1<x2.
当x变化时,F′(x)、F(x)的变化情况如下:
X | (-∞, |
| ( | 0 | (0,+∞) |
F′(x) | + | 0 | - | 0 | + |
F(x) | 增函数 | 极大值 | 减函数 | 极小值 | 增函数 |
∴当x=0时,F(x)取得极小值4.
(2)由(1)知F(x)=x3+(2-a)x2+4.∵F(x)≥0在[0,+∞)上恒成立![]() 当x∈[0,+∞)时,F(x)min≥0.
当x∈[0,+∞)时,F(x)min≥0.
①若2-a>0,即a<2时,由(1)可知F(x)min=F(0)=4>0,符合题意;
②若2-a≤0,即a≥2时,由F′(x)=0求得x1=![]() ,x2=0,且x1>x2.
,x2=0,且x1>x2.
∴当x∈[0,+∞)时,F(x)min=F(![]() )≥0,即(
)≥0,即(![]() )3-(a-2)(
)3-(a-2)(![]() )2+4≥0,解不等式得2≤a≤5.综上所述,应有a≤5.
)2+4≥0,解不等式得2≤a≤5.综上所述,应有a≤5.
要证不等式a2-13a+39≥![]() ,只需证6-a+
,只需证6-a+![]() ≥-(a-6)2+3.∵a≤5,∴6-a+
≥-(a-6)2+3.∵a≤5,∴6-a+![]() ≥2,
≥2,
-(a-6)2+3≤2.(当a=5时,“=”成立)故a2-13a+39≥![]() 成立(当a=5时,“=”成立).
成立(当a=5时,“=”成立).


 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案科目:高中数学 来源: 题型:

 (理)已知函数f(x)=
(理)已知函数f(x)=| ln(2-x2) |
| |x+2|-2 |
| AB |
| AD |
查看答案和解析>>
科目:高中数学 来源: 题型:
| sin2x-(a-4)(sinx-cosx)+a |
| π |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
|
查看答案和解析>>
科目:高中数学 来源: 题型:
 (2011•普陀区三模)(理)已知函数f(x)=
(2011•普陀区三模)(理)已知函数f(x)=| ln(2-x2) | |x+2|-2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| ||
| 1-x |
| 1 |
| n |
| 2 |
| n |
| n-1 |
| n |
| 1 |
| a1 |
| 1 |
| a2 |
| 1 |
| an |
| sinα | ||
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com