方程x+y+z=12的正整数解的个数为________.
55
分析:利用已知条件方程x+y+z=12的正整数解,得出x,y,z的取值范围,列出所有的可能即可.
解答:根据已知条件
∵x+y+z=12,且x、y、z∈Z+
∴1≤x≤10,1≤y≤10,1≤z≤10,
列出所有的可能:
当x=1时,y可以取1,2,3,4,5,6,7,8,9,10,共10种情况;
当x=2时,y可以取1,2,3,4,5,6,7,8,9,共9种情况;
当x=3时,y可以取1,2,3,4,5,6,7,8,共8种情况;
当x=4时,y可以取1,2,3,4,5,6,7,共7种情况;
当x=5时,y可以取1,2,3,4,5,6,共6种情况;
当x=6时,y可以取1,2,3,4,5,共5种情况;
当x=7时,y可以取1,2,3,4,共4种情况;
当x=8时,y可以取1,2,3,共3种情况;
当x=9时,y可以取1,2,共2种情况;
当x=10时,y可以取1,共1种情况;
所以共有10+9+8+7+6+5+4+3+2+1=55组.
故答案为:55
点评:本题的考点是进行简单的合情推理,解题的关键是利用已知条件方程x+y+z=12的正整数解,得出x,y,z的取值范围



 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案 (2012•江苏二模)选做题
(2012•江苏二模)选做题 .
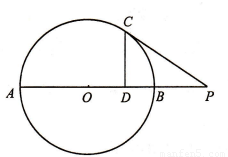
.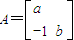 把直线l:y=2x-4变换为直线l′:y=x-12,求a,b的值.
把直线l:y=2x-4变换为直线l′:y=x-12,求a,b的值. =1上的点P到直线l:3x+4y+18=0的距离的最小值.
=1上的点P到直线l:3x+4y+18=0的距离的最小值.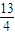 ,求x+y+z的最大值.
,求x+y+z的最大值.