练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    10．已知数列{an}为等差数列，a1=35，d=-2，Sn=0，则n=36．

    分析 直接把已知代入等差数列的前n项和得答案．

    解答 解：在等差数列{an}中，由a1=35，d=-2，Sn=0，得
    ${S}_{n}=35n+\frac{n（n-1）}{2}×（-2）=0$，解得n=0（舍）或n=36．
    故答案为：36．

    点评 本题考查等差数列的前n项和，是基础的计算题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    20．P点在则△ABC所在的平面外，O点是P点在平面ABC内的射影，PA、PB、PC两两垂直，则D点是则△ABC的垂心．（填外心，内心，垂心，重心）

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    1．已知定义为R的函数f（x）满足下列条件：（1）对任意的实数x，y都有：f（x+y）=f（x）+f（y）-1，（2）当x＞0时，f（x）＞1．
    （1）求f（0）；
    （2）求证：f（x）在R上为增函数；
    （3）若f（6）=7，a≤-3，关于x的不等式f（ax-2）+f（x-x2）＜3对任意的x∈[-1，+∞）恒成立，求实数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    18．在直角坐标系平面中，已知点P1（1，2），P2（2，22），P3（3，23），…，Pn（n，2n），其中n是正整数，对于平面上任意一点A0，记A1为A0关于点P1的对称点，A2为A1关于点P2的对称点，…，An为An-1关于点Pn的对称点，则对任意偶数n，用n表示向量$\overrightarrow{{A}_{0}{A}_{n}}$的坐标为（　　）
    A．（n，$\frac{4（{2}^{n}-1）}{3}$）B．（n，$\frac{{2}^{n+2}}{3}$）C．（$\frac{n}{2}$，$\frac{2（{2}^{n}-1）}{3}$）D．（$\frac{n}{2}$，$\frac{{2}^{n+1}}{3}$）

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    5．已知P（-1，1），Q（2，2），若直线l：y=mx-1与射线PQ（P为端点）有交点，则实数m的取值范围是m≤-2或m＞$\frac{1}{3}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

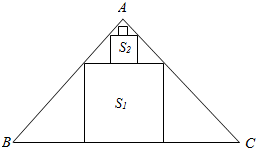    15．在等腰直角△ABC中，∠A=90°，BC=6，△ABC中排列着内接正方形，如图所示，若正方形的面积依次为S1，S2，…，Sn，…（从大到小），其中n∈N+，则$\underset{lim}{n→∞}$（S1+S2+…+Sn）=$\frac{9}{2}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

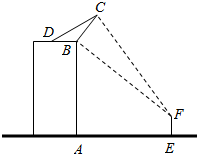    2．如图，一楼房高AB为19$\sqrt{3}$米，某广告公司在楼顶安装一块宽BC为4米的广告牌，CD为拉杆，广告牌的倾角为60°，安装过程中，一身高为$\sqrt{3}$米的监理人员EF站在楼前观察该广传牌的安装效果：为保证安全，该监理人员不得站在广告牌的正下方：设AE=x米，该监理人员观察广告牌的视角∠BFC=θ．
    （1）试将tanθ表示为x的函数；
    （2）求点E的位置，使θ取得最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    19．记x=log34•log56•log78，y=log45•log67•log89，则xy=2．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    20．求函数y=$\sqrt{lo{g}_{2}（4x-3）}$的定义域．

    查看答案和解析>>

    同步练习册答案