
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,短轴长为
,短轴长为![]() ,右焦点为
,右焦点为![]() (1) 求椭圆
(1) 求椭圆![]() 的标准方程;(2) 若直线
的标准方程;(2) 若直线![]() 经过点
经过点![]() 且与椭圆
且与椭圆![]() 有且仅有一个公共点
有且仅有一个公共点![]() ,过点
,过点![]() 作直线
作直线![]() 交椭圆于另一点
交椭圆于另一点![]() ①证明:当直线
①证明:当直线![]() 与直线
与直线![]() 的斜率
的斜率![]() ,
,![]() 均存在时,
均存在时,![]() .
.![]() 为定值;②求
为定值;②求![]() 面积的最小值。
面积的最小值。
【答案】(1)![]() (2) ①见解析②
(2) ①见解析②![]()
【解析】
(1)根据条件列关于a,b,c的方程组解得a,b,即得结果,(2) ①先设直线![]() 方程:
方程:![]() ,再根据直线与椭圆相切得
,再根据直线与椭圆相切得![]() 关系,并解得P点坐标,最后根据斜率公式计算
关系,并解得P点坐标,最后根据斜率公式计算![]() .
.![]() 为定值,②先确定三角形为直角三角形,再利用弦长公式计算PQ,根据面积公式得函数关系式,最后根据函数单调性确定最小值.
为定值,②先确定三角形为直角三角形,再利用弦长公式计算PQ,根据面积公式得函数关系式,最后根据函数单调性确定最小值.
解:(1)由题意得![]() ,
,
所以椭圆方程为![]()
(2)①证明:由题意知直线![]() 的斜率存在,设直线
的斜率存在,设直线![]() 的方程为
的方程为![]() ,
,
因为点![]() 在直线上,则
在直线上,则![]() ,
,
联立直线与椭圆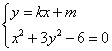 可得
可得![]()
因为直线与椭圆只有一个交点,所以![]() ,即
,即![]() ,
,
由韦达定理得![]() ,
,
又因为![]() 过右焦点
过右焦点![]() ,则
,则![]()
![]()
而![]() ,所以
,所以![]() .
.![]()
②因为F(2,0),所以![]() ,
,![]()
![]() ,所以
,所以![]() ,即
,即![]() ,
,
所以三角形的面积![]() ,
,![]() ,
,
因为![]() ,所以
,所以![]() 方程为
方程为![]() ,设
,设![]()
![]()
与椭圆方程联立 得
得![]() ,
,
则![]() ,
,![]() ,
,![]() ,
,
所以![]()
令![]() ,则
,则![]() ,令
,令![]() ,因此当
,因此当![]()
![]() 时,
时,![]() 面积取最小值
面积取最小值![]() .
.


科目:高中数学 来源: 题型:
【题目】如图,在三棱锥P﹣ABC中,△ABC是边长为2的正三角形,∠PCA=90°,E,H分别为AP,AC的中点,AP=4,BE=![]() .
.
(Ⅰ)求证:AC⊥平面BEH;
(Ⅱ)求直线PA与平面ABC所成角的正弦值.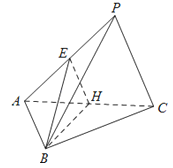
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正四棱柱ABCD-A1B1C1D1中,底面边长为2![]() ,侧棱长为4,E,F分别是棱AB,BC的中点,EF∩BD=G.求证:平面B1EF⊥平面BDD1B1.
,侧棱长为4,E,F分别是棱AB,BC的中点,EF∩BD=G.求证:平面B1EF⊥平面BDD1B1.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知A、B、C、D是函数y=sin(ωx+φ)(ω>0,0<φ<![]() )一个周期内的图象上的四个点,如图所示,A(﹣
)一个周期内的图象上的四个点,如图所示,A(﹣![]() , 0),B为y轴的点,C为图象上的最低点,E为该函数图象的一个对称中心,B与D关于点E对称,
, 0),B为y轴的点,C为图象上的最低点,E为该函数图象的一个对称中心,B与D关于点E对称,![]() 在x轴方向上的投影为
在x轴方向上的投影为![]() .
.
(1)求函数f(x)的解析式及单调递减区间;
(2)将函数f(x)的图象向左平移![]() 得到函数g(x)的图象,已知g(α)=
得到函数g(x)的图象,已知g(α)=![]() , α∈(﹣
, α∈(﹣![]() , 0),求g(α+
, 0),求g(α+![]() )的值.
)的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥P﹣ABC中,PA=PB=AB=BC=2,∠CBA=∠PBC=60°,Q为线段BC的中点.
(1)求证:PA⊥BC;
(2)求点Q到平面PAC的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,边长为![]() 的正方形ADEF与梯形ABCD所在的平面互相垂直,其中AB∥CD,AB⊥BC,DC=BC=
的正方形ADEF与梯形ABCD所在的平面互相垂直,其中AB∥CD,AB⊥BC,DC=BC=![]() AB=1,点M在线段EC上.
AB=1,点M在线段EC上.
(Ⅰ)证明:平面BDM⊥平面ADEF;
(Ⅱ)判断点M的位置,使得三棱锥B﹣CDM的体积为![]() .
. 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】用6种颜色给右图四面体A﹣BCD的每条棱染色,要求每条棱只染一种颜色且共顶点的棱染不同的颜色,则不同的染色方法共有( )种. 
A.4080
B.3360
C.1920
D.720
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com