
分析 由题意求出双曲线方程,再由向量等式可得∠MF1A=∠MF1B,求出PF1所在直线的斜率,得到PF1所在直线的方程,联立直线方程和双曲线方程,求出P的坐标,进一步说明M为△PF1F2内切圆的圆心,然后由三角形面积差结合双曲线定义求得答案.
解答 解:如图,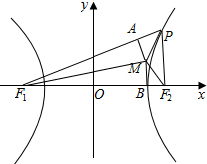
由椭圆$\frac{x^2}{9}+\frac{y^2}{5}=1$,得a=3,$c=\sqrt{{a}^{2}-{b}^{2}}=2$,
∴双曲线的实轴长为4,焦距长为6,双曲线方程为$\frac{{x}^{2}}{4}-\frac{{y}^{2}}{5}=1$.
由$\frac{{\overrightarrow{P{F_1}}•\overrightarrow{M{F_1}}}}{{|{\overrightarrow{P{F_1}}}|}}=\frac{{\overrightarrow{{F_2}{F_1}}•\overrightarrow{M{F_1}}}}{{|{\overrightarrow{{F_2}{F_1}}}|}}$,可得
$\overrightarrow{M{F}_{1}}$在$\overrightarrow{P{F}_{1}}$与$\overrightarrow{{F}_{2}{F}_{1}}$方向上的投影相等,即|F1A|=|F1B|,
∴∠MF1A=∠MF1B,
而tan$∠M{F}_{1}A=\frac{MA}{{F}_{1}A}=\frac{1}{5}$,
∴tan∠PF1A=$\frac{2tan∠M{F}_{1}A}{1-ta{n}^{2}∠M{F}_{1}A}$=$\frac{\frac{2}{5}}{1-\frac{1}{25}}=\frac{5}{12}$.
∴直线F1P的方程为y=$\frac{5}{12}$(x+3),即5x-12y+15=0.
联立$\left\{\begin{array}{l}{5x-12y+15=0}\\{\frac{{x}^{2}}{4}-\frac{{y}^{2}}{5}=1}\end{array}\right.$,解得P($3,\frac{5}{2}$),
∴PF2⊥x轴,
又tan∠MF2O=1,∴∠MF2O=45°,即M为△PF1F2内切圆的圆心.
则${S_{△PM{F_1}}}-{S_{△PM{F_2}}}$=$\frac{1}{2}$(|PF1|-|PF2|)×1=$\frac{1}{2}×4=2$,
故答案为:2.
点评 本题考查椭圆的简单性质,考查了向量在向量方向上的投影,考查计算能力,是中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
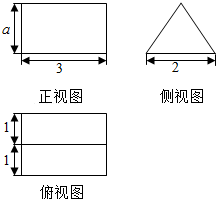 如图是一个几何体的三视图,若它的体积是3$\sqrt{3}$,则a=$\sqrt{3}$,该几何体的表面积为2$\sqrt{3}$+18.
如图是一个几何体的三视图,若它的体积是3$\sqrt{3}$,则a=$\sqrt{3}$,该几何体的表面积为2$\sqrt{3}$+18.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com