
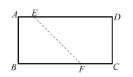
【题目】如图,在矩形![]() 中,
中,![]() 分别在
分别在![]() 上,且
上,且![]() ,沿
,沿![]() 将四边形
将四边形![]() 折成四边形
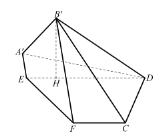
折成四边形![]() ,使点
,使点![]() 在平面
在平面![]() 上的射影
上的射影![]() 在直线
在直线![]() 上
上
(1)求证:平面![]() 平面
平面![]() ;
;
(2)求证:![]() 平面
平面![]() ;
;
(3)求二面角![]() 的正弦值
的正弦值
【答案】(1)证明见解析;(2)证明见解析;(3)![]()
【解析】
(1)![]() 平面
平面![]() ,证明故
,证明故![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,得到证明.
,得到证明.
(2)![]() ,
,![]() 得到平面
得到平面![]() 平面
平面![]() ,得到证明.
,得到证明.
(3)以![]() 为
为![]() 轴,平面
轴,平面![]() 内与
内与![]() 垂直的直线为
垂直的直线为![]() 轴,平面
轴,平面![]() 内与
内与![]() 垂直的直线为
垂直的直线为![]() 轴,建立空间直角坐标系,计算
轴,建立空间直角坐标系,计算![]() ,根据
,根据![]() 得到
得到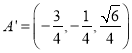 ,平面
,平面![]() 的法向量为
的法向量为![]() ,平面
,平面![]() 的一个法向量为
的一个法向量为![]() ,计算夹角得到答案.
,计算夹角得到答案.
(1)![]() 在平面
在平面![]() 上的射影
上的射影![]() 在直线
在直线![]() 上,故
上,故![]() 平面
平面![]() .
.
![]() 平面
平面![]() ,故
,故![]() ,
,![]() ,
,![]() ,故
,故![]() 平面
平面![]() .
.
![]() 平面
平面![]() ,故平面
,故平面![]() 平面
平面![]() .
.
(2)![]() ,故
,故![]() ,
,![]() 平面
平面![]() ,故
,故![]() 平面
平面![]() .
.
![]() ,
,![]() 平面
平面![]() ,故
,故![]() 平面
平面![]() ,
,![]() .
.
故平面![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,故
,故![]() 平面
平面![]() .
.
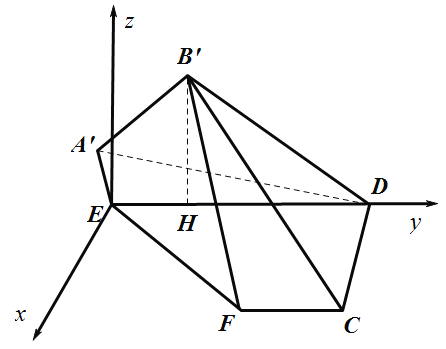
(3)如图所示:以![]() 为
为![]() 轴,平面
轴,平面![]() 内与
内与![]() 垂直的直线为
垂直的直线为![]() 轴,平面
轴,平面![]() 内与
内与![]() 垂直的直线为
垂直的直线为![]() 轴,建立空间直角坐标系.
轴,建立空间直角坐标系.
![]() ,
,![]() ,
,![]() ,设
,设![]() ,
,![]() ,
,
![]() ,取正解,得到
,取正解,得到![]() ,
,![]() ,故
,故![]() .
.
![]() ,故
,故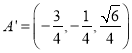 ,
,
设平面![]() 的法向量为
的法向量为![]() ,故
,故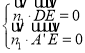 ,即
,即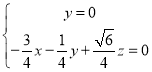 ,
,
取![]() ,得到
,得到![]() ,故
,故![]() .
.
易知:平面![]() 的一个法向量为
的一个法向量为![]() ,故
,故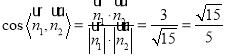 .
.
故二面角![]() 的正弦值为
的正弦值为![]() .
.


科目:高中数学 来源: 题型:
【题目】在2019年女排世界杯中,中国女排与巴西女排对垒中采用“五局三胜”制,即哪个队先胜三场即获得胜利.根据以往比赛数据统计,中国女排每局获胜概率为![]() ,巴西女排每局获胜概率为
,巴西女排每局获胜概率为![]() .
.
(1)中国女排战胜巴西女排的概率;
(2)比赛中中国女排第一局获胜,在该条件下求比赛总局数![]() 的分布列及
的分布列及![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解春季昼夜温差大小与某种子发芽数之间的关系,现在从4月份的30天中随机挑选了5天进行研究,且分别记录了明天昼夜温差与每天100颗种子浸泡后的发芽数,得到如下表格:
日期 | 4月1日 | 4月7日 | 4月15日 | 4月21日 | 4月30日 |
温差x/℃ | 10 | 11 | 13 | 12 | 8 |
发芽数y/颗 | 23 | 25 | 30 | 26 | 16 |
从这5天中任选2天,记发芽的种子数分别为![]() ,求事件“
,求事件“![]() 君不小于25”的概率;
君不小于25”的概率;
(2)从这5天中任选2天,若选取的是4月1日与4月30日的两组数据,请根据这5填中的另三天的数据,求出![]() 关于
关于![]() 的线性回归方程,
的线性回归方程,![]() .
.
(参考公式: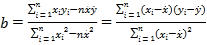 ,
,![]() ).
).
查看答案和解析>>
科目:高中数学 来源: 题型:
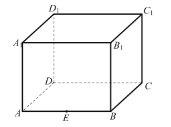
【题目】已知正四棱柱![]() 的底面边长
的底面边长![]() ,侧棱长
,侧棱长![]() ,它的外接球的球心为
,它的外接球的球心为![]() ,点
,点![]() 是
是![]() 的中点,点
的中点,点![]() 是球
是球![]() 上的任意一点,有以下命题:
上的任意一点,有以下命题:
①![]() 的长的最大值为9;
的长的最大值为9;
②三棱锥![]() 的体积的最大值是
的体积的最大值是![]() ;
;
③存在过点![]() 的平面,截球
的平面,截球![]() 的截面面积为
的截面面积为![]() ;
;
④三棱锥![]() 的体积的最大值为20;
的体积的最大值为20;
⑤过点![]() 的平面截球
的平面截球![]() 所得的截面面积最大时,
所得的截面面积最大时,![]() 垂直于该截面.
垂直于该截面.
其中是真命题的序号是___________
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】电动摩托车的续航里程,是指电动摩托车在蓄电池满电量的情况下一次能行驶的最大距离.为了解A,B两个不同型号电动摩托车的续航里程,现从某卖场库存电动摩托车中随机抽取A,B两个型号的电动摩托车各5台,在相同条件下进行测试,统计结果如下:
电动摩托车编号 | 1 | 2 | 3 | 4 | 5 |
A型续航里程(km) | 120 | 125 | 122 | 124 | 124 |
B型续航里程(km) | 118 | 123 | 127 | 120 | a |
已知A,B两个型号被测试电动摩托车续航里程的平均值相等.
(1)求a的值;
(2)求A型号被测试电动摩托车续航里程标准差的大小;
(3)从被测试的电动摩托车中随机抽取A,B型号电动摩托车各1台,求至少有1台的续航里程超过122km的概率.
(注:n个数据![]() ,的方差
,的方差![]() ,其中
,其中![]() 为数据
为数据![]() 的平均数)
的平均数)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】海水养殖场进行某水产品的新、旧网箱养殖方法的产量对比,收获时各随机抽取了![]() 个网箱,测量各水箱产品的产量(单位:kg),其频率分布直方图如下图所示.
个网箱,测量各水箱产品的产量(单位:kg),其频率分布直方图如下图所示.

(1)若用频率视为概率,记![]() 表示事件“旧养殖法的箱产量低于
表示事件“旧养殖法的箱产量低于![]() kg”,求事件
kg”,求事件![]() 的概率;
的概率;
(2)填写以下![]() 列联表,并根据此判断是否有
列联表,并根据此判断是否有![]() 的把握认为箱产量与养殖方法有关?
的把握认为箱产量与养殖方法有关?
箱产量 | 箱产量 | 合计 | |
旧养殖方法 | |||
新养殖方法 | |||
合计 |
(3)根据箱产量频率分布直方图,求新养殖法箱产量的中位数的估计值(精确到![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分12分)已知点![]() 为抛物线
为抛物线![]() 的焦点,点
的焦点,点![]() 在抛物线
在抛物线![]() 上,且
上,且![]() .
.

(Ⅰ)求抛物线![]() 的方程;
的方程;
(Ⅱ)已知点![]() ,延长
,延长![]() 交抛物线
交抛物线![]() 于点
于点![]() ,证明:以点
,证明:以点![]() 为圆心且与直线
为圆心且与直线![]() 相切的圆,必与直线
相切的圆,必与直线![]() 相切.
相切.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知10件不同产品中有3件是次品,现对它们一一取出(不放回)进行检测,直至取出所有次品为止.
(1)若恰在第5次取到第一件次品,第10次才取到最后一件次品,则这样的不同测试方法数有多少?
(2)若恰在第6次取到最后一件次品,则这样的不同测试方法数是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com