练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】下列说法正确的是（ ）

    A.抛掷一枚硬币，正面朝上的概率是，所以抛掷两次一定会出现一次正面朝上的情况

    B.某地气象局预报说，明天本地降水概率为，这说明明天本地有的区域下雨

    C.概率是客观存在的，与试验次数无关

    D.若买彩票中奖的概率是万分之一，则买彩票一万次就有一次中奖

    【答案】C

    【解析】

    概率是反映事件发生机会的大小的概率，只是表示发生机会的大小，机会大也不一定发生.

    解：对于A，这是一个随机事件，抛掷一枚硬币，出现正面朝上或者反面朝上都有可能，事先无法预料，错误；

    对于B，这是一个随机事件，明天本地降水概率为表示明天有的可能降雨，事先无法预料，错误；

    对于C，正确；

    对于D，这是一个随机事件，买彩票中奖或不中奖都有可能，事先无法预料，错误.

    故选：C.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】“水资源与永恒发展”是2015年联合国世界水资源日主题．近年来，某企业每年需要向自来水厂缴纳水费约4万元，为了缓解供水压力，决定安装一个可使用4年的自动污水净化设备，安装这种净水设备的成本费（单位：万元）与管线、主体装置的占地面积（单位：平方米）成正比，比例系数约为0．2．为了保证正常用水，安装后采用净水装置净水和自来水厂供水互补的用水模式．假设在此模式下，安装后该企业每年向自来水厂缴纳的水费 C（单位：万元）与安装的这种净水设备的占地面积x（单位：平方米）之间的函数关系是（x≥0，k为常数）．记y为该企业安装这种净水设备的费用与该企业4年共将消耗的水费之和．

    （1） 试解释的实际意义，请建立y关于x的函数关系式并化简;

    （2） 当x为多少平方米时，y取得最小值？最小值是多少万元？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知定义域为R的函数f（x）=是奇函数．

    （1）求b的值，判断并用定义法证明f（x）在R上的单调性；

    （2）解不等式f（2x+1）+f（x）＜0．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数.

    ⑴若函数的图象经过点，求实数的值.

    ⑵当时，函数的最小值为1，求当时，函数最大值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如果f（x）是定义在R上的函数，且对任意的x∈R，均有f（-x）≠-f（x），则称该函数是“X—函数”.

    （1）分别判断下列函数：①y=；②y=x+1；③y=x2+2x-3是否为“X—函数”？（直接写出结论）

    （2）若函数f（x）=x-x2+a是“X—函数”，求实数a的取值范围；

    （3）设“X—函数”f（x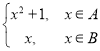）=在R上单调递增，求所有可能的集合A与B.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在四棱锥中，底面为平行四边形，已知，，于.

    （1）求证：；

    （2）若平面平面，且，求二面角的余弦值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知二次函数f(x)满足f(x＋1)－f(x)＝－2x＋1，且f(2)＝15.

    (1)求函数f(x)的解析式；

    (2) 令g(x)＝(2－2m)x－f(x)．

    ① 若函数g(x)在x∈[0，2]上是单调函数，求实数m的取值范围；

    ② 求函数g(x)在x∈[0，2]上的最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

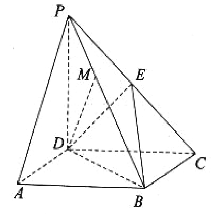
    【题目】如图，在四棱锥中，底面是平行四边形，平面，，，是棱上的一点.

    （1）若平面，证明：；

    （2）在（1）的条件下，棱上是否存在点，使直线与平面所成角的大小为？若存在，求的值；若不存在，请说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知过点的直线与椭圆：交于不同的两点，其中，为坐标原点．

    （1）若，求的面积；

    （2）在轴上是否存在定点，使得直线与的斜率互为相反数？

    查看答案和解析>>

    同步练习册答案