
 在圆x2+y2=4上任取一点P,过点P作x轴的垂线段PD,D为垂足.当点P在圆上运动时,线段PD的中点M的轨迹记作曲线C.
在圆x2+y2=4上任取一点P,过点P作x轴的垂线段PD,D为垂足.当点P在圆上运动时,线段PD的中点M的轨迹记作曲线C.分析 (1)设P(x0,y0),M(x,y),D(x0,0),由M是PD的中点,可得$\left\{\begin{array}{l}{{x}_{0}=x}\\{{y}_{0}=2y}\end{array}\right.$,又P在圆x2+y2=4上,可得x02+y02=4,代入化简即可得出.
(2)设|MF1|=m,|MF2|=n,则m+n=2a=4,m2+n2=(2c)2=12,联立解得mn,即可得出.
解答 解:(1)设P(x0,y0),M(x,y),D(x0,0),∵M是PD的中点,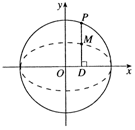
∴$\left\{\begin{array}{l}{{x}_{0}=x}\\{{y}_{0}=2y}\end{array}\right.$,又P在圆x2+y2=4上,
∴x02+y02=4,即x2+4y2=4,$\frac{{x}^{2}}{4}$+y2=1.
∴线段PD的中点M的轨迹方程是$\frac{{x}^{2}}{4}$+y2=1.
(2)设|MF1|=m,|MF2|=n,则m+n=2a=4,m2+n2=(2c)2=12,
联立解得mn=1,
∴三角形△MF1F2的面积${S_{△M{F_1}{F_2}}}$=$\frac{1}{2}$mn=$\frac{1}{2}$.
点评 本题考查了椭圆的定义标准方程及其性质、勾股定理、三角形面积计算公式,考查了推理能力与计算能力,属于中档题.


 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 6 | B. | 7 | C. | 8 | D. | 9 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com