
| A. | $\frac{5\sqrt{3}}{3}$ | B. | 3 | C. | 2或3 | D. | -$\frac{\sqrt{3}}{3}$或$\frac{5\sqrt{3}}{3}$ |
分析 可由条件求出$|\overrightarrow{a}-\overrightarrow{b}{|}^{2}=14-2\overrightarrow{a}•\overrightarrow{b}$,进而得出$|\overrightarrow{a}-\overrightarrow{b}|$的值,并可由$\overrightarrow{a}•(\overrightarrow{a}-\overrightarrow{b})={\overrightarrow{a}}^{2}-\overrightarrow{a}•\overrightarrow{b}$和$\overrightarrow{a}•(\overrightarrow{a}-\overrightarrow{b})=|\overrightarrow{a}||\overrightarrow{a}-\overrightarrow{b}|•\frac{\sqrt{3}}{3}$建立关于$\overrightarrow{a}•\overrightarrow{b}$的方程,从而求出$\overrightarrow{a}•\overrightarrow{b}$,根据投影的计算公式便可求出所求投影的值.
解答 解:根据条件,$|\overrightarrow{a}-\overrightarrow{b}{|}^{2}={\overrightarrow{a}}^{2}-2\overrightarrow{a}•\overrightarrow{b}+{\overrightarrow{b}}^{2}$=14$-2\overrightarrow{a}•\overrightarrow{b}$;
∴$|\overrightarrow{a}-\overrightarrow{b}|=\sqrt{14-2\overrightarrow{a}•\overrightarrow{b}}$;
又∵$\overrightarrow{a}•(\overrightarrow{a}-\overrightarrow{b})={\overrightarrow{a}}^{2}-\overrightarrow{a}•\overrightarrow{b}=3-\overrightarrow{a}•\overrightarrow{b}$,
$\overrightarrow{a}•(\overrightarrow{a}-\overrightarrow{b})=|\overrightarrow{a}||\overrightarrow{a}-\overrightarrow{b}|cos<\overrightarrow{a},\overrightarrow{a}-\overrightarrow{b}>$=$\sqrt{14-2\overrightarrow{a}•\overrightarrow{b}}$;
∴$3-\overrightarrow{a}•\overrightarrow{b}=\sqrt{14-2\overrightarrow{a}•\overrightarrow{b}}$;
解得$\overrightarrow{a}•\overrightarrow{b}=5$或$\overrightarrow{a}•\overrightarrow{b}$=-1,
又∵向量$\overrightarrow{a}$,$\overrightarrow{b}$的夹角为锐角,
∴$\overrightarrow{a}•\overrightarrow{b}=5$,
∴$\overrightarrow{b}$在$\overrightarrow{a}$方向上的投影为$|\overrightarrow{b}|cos<\overrightarrow{a},\overrightarrow{b}>=|\overrightarrow{b}|•\frac{\overrightarrow{a}•\overrightarrow{b}}{|\overrightarrow{a}||\overrightarrow{b}|}=\frac{\overrightarrow{a}•\overrightarrow{b}}{|\overrightarrow{a}|}$=$\frac{5}{\sqrt{3}}=\frac{5\sqrt{3}}{3}$.
故选A.
点评 考查向量数量积的运算,以及要求$|\overrightarrow{a}-\overrightarrow{b}|$而求$(\overrightarrow{a}-\overrightarrow{b})^{2}$的方法,以及一元二次方程的解法,一个向量在另一个向量方向上投影的计算公式.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | ($\overrightarrow{a}$•$\overrightarrow{b}$)•$\overrightarrow{c}$=$\overrightarrow{a}$•($\overrightarrow{b}$•$\overrightarrow{c}$) | B. | $\overrightarrow{a}$•$\overrightarrow{b}$=$\overrightarrow{a}$•$\overrightarrow{c}$,则$\overrightarrow{b}$=$\overrightarrow{c}$ | ||
| C. | |$\overrightarrow{a}$•$\overrightarrow{b}$|=|$\overrightarrow{a}$|•|$\overrightarrow{b}$| | D. | 若|$\overrightarrow{a}$+$\overrightarrow{b}$|=|$\overrightarrow{a}$-$\overrightarrow{b}$|,则$\overrightarrow{a}$•$\overrightarrow{b}$=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{11}{2}$ | B. | $\frac{11}{2}$ | C. | -$\frac{29}{2}$ | D. | $\frac{29}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
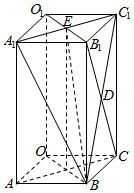 如图,已知ABCO-A1B1C1O1为长方体,OA=OC=2,OO1=4,D为BC1与B1C的交点,E为A1C1与B1O1的交点,求二面角D-A1C1-A的平面角的正切值.
如图,已知ABCO-A1B1C1O1为长方体,OA=OC=2,OO1=4,D为BC1与B1C的交点,E为A1C1与B1O1的交点,求二面角D-A1C1-A的平面角的正切值.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com