
【题目】执行如图所示的程序框图,输出的结果是( ) 
A.﹣2
B.![]()
C.![]()
D.3
【答案】C
【解析】解:模拟执行程序,可得
a= ![]() ,k=0
,k=0
执行循环体,a=3,k=1
不满足条件k≥100,执行循环体,a=﹣2,k=2
不满足条件k≥100,执行循环体,a=﹣ ![]() ,k=3
,k=3
不满足条件k≥100,执行循环体,a= ![]() ,k=4
,k=4
…
观察规律可得a的取值周期为4,由于99=24×4+3,可得
不满足条件k≥100,执行循环体,a= ![]() ,k=100,
,k=100,
此时,满足条件k≥100,退出循环,输出a的值为 ![]() .
.
故选:C.
【考点精析】解答此题的关键在于理解程序框图的相关知识,掌握程序框图又称流程图,是一种用规定的图形、指向线及文字说明来准确、直观地表示算法的图形;一个程序框图包括以下几部分:表示相应操作的程序框;带箭头的流程线;程序框外必要文字说明.


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=![]() -2
-2![]() +lnx.
+lnx.
(Ⅰ)若a=1,求函数f(x)的极值;
(Ⅱ)若函数f(x)在区间[1,2]上为单调递增函数,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知正方形ABCD和矩形ACEF所在的平面互相垂直,AB= ![]() ,AF=1,M是线段EF的中点.
,AF=1,M是线段EF的中点. 
(1)求证AM∥平面BDE;
(2)求二面角A﹣DF﹣B的大小;
(3)试在线段AC上一点P,使得PF与CD所成的角是60°.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着网络时代的进步,流量成为手机的附带品,人们可以利用手机随时随地的浏览网页,聊天,看视频,因此,社会上产生了很多低头族.某研究人员对该地区18∽50岁的5000名居民在月流量的使用情况上做出调查,所得结果统计如下图所示:
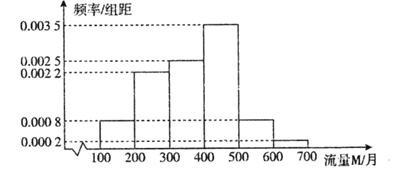
(Ⅰ)以频率估计概率,若在该地区任取3位居民,其中恰有![]() 位居民的月流量的使用情况
位居民的月流量的使用情况
在300M∽400M之间,求![]() 的期望
的期望![]() ;
;
(Ⅱ)求被抽查的居民使用流量的平均值;
(Ⅲ)经过数据分析,在一定的范围内,流量套餐的打折情况![]() 与其日销售份数
与其日销售份数![]() 成线性相关
成线性相关
关系,该研究人员将流量套餐的打折情况![]() 与其日销售份数
与其日销售份数![]() 的结果统计如下表所示:
的结果统计如下表所示:
折扣 | 1折 | 2折 | 3折 | 4折 | 5折 |
销售份数 | 50 | 85 | 115 | 140 | 160 |
试建立![]() 关于
关于![]() 的的回归方程.
的的回归方程.
附注:回归方程![]() 中斜率和截距的最小二乘估计公式分别为:
中斜率和截距的最小二乘估计公式分别为:
 ,
, ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题中正确的是( )
A.若ξ服从正态分布N(0,2),且P(ξ>2)=0.4,则P(0<ξ<2)=0.2
B.x=1是x2﹣x=0的必要不充分条件
C.直线ax+y+2=0与ax﹣y+4=0垂直的充要条件为a=±1
D.“若xy=0,则x=0或y=0”的逆否命题为“若x≠0或y≠0,则xy≠0”
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分12分) 命题![]() 实数x满足
实数x满足![]() (其中
(其中![]() ),命题
),命题![]() 实数
实数![]() 满足
满足
(Ⅰ)若![]() ,且
,且![]() 为真,求实数
为真,求实数![]() 的取值范围;
的取值范围;
(Ⅱ)若![]() 是
是![]()
![]() 的充分不必要条件,求实数a的取值范围.
的充分不必要条件,求实数a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com