已知:函数f(x)=[x[x]](x∈R),其中[x]表示不超过x的最大整数.
如[-2.1]=-3,[-3]=-3,[2.5]=2.
(1)判断f(x)的奇偶性;
(2)若x∈[-2,3],求f(x)的值域;
(3)若x∈[0,n](n∈N*),f(x)的值域为An,现将An,中的元素的个数记为an.试求an+1与an的关系,并进一步求出an的表达式.
【答案】
分析:(1)根据函数f(x)=[x[x]](x∈R)的定义可得:f(-

)≠f(

),f(-

)≠-f(

),故f(x)为非奇非偶函数;
(2)先对x的取值进行分类讨论:当-2≤x<-1时;当-1≤x<0时;当0≤x<1时;当1≤x<2时;当2≤x<3时;故所求f(x)的值域为{0,1,2,3,4,5,9};
(3)分类讨论:当n<x<n+1时;当x=n+1时;因此,可得a
n+1=a
n+n,又由(2)知,a
1=2,利用a
n=(a
2-a
1)+(a
3-a
2)+…+(a
n-a
n-1)+a
1求出a
n的表达式即可.
解答:解:(1)∵f(

)=[

[

]]=[

•1]=[

]=1,
f(-

)=[-

[-

]]=[-

•(-2)]=[3]=3,
∴f(-

)≠f(

),f(-

)≠-f(

),故f(x)为非奇非偶函数.(4分)
(2)当-2≤x<-1时,[x]=-2,则2<x[x]≤4,∴f(x)可取2,3,4;
当-1≤x<0时,[x]=-1,则0<x[x]≤1,∴f(x)可取0,1;
当0≤x<1时,[x]=0,则x[x]=0,∴f(x)=0;
当1≤x<2时,[x]=1,则1≤x[x]<2,∴f(x)=1;
当2≤x<3时,[x]=2,则4≤x[x]<6,∴f(x)可取4,5;
又f(3)=[3[3]]=9,
故所求f(x)的值域为{0,1,2,3,4,5,9},(9分)
(3)当n<x<n+1时,[x]=n,则 n
2<x[x]<n(n+1),
故f(x)可取n
2,n
2+1,n
2+2,…,n
2+n-1,
当x=n+1时,f(n+1)=(n+1)
2,
又当x∈[0,n]时,显然有f(x)≤n
2.
因此,可得a
n+1=a
n+n,又由(2)知,a
1=2,
∴a
n=(a
2-a
1)+(a
3-a
2)+…+(a
n-a
n-1)+a
1=(2-1)+(3-1)+(4-1)+1…+(n-1)+2
=
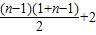
=
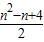
(14分)
点评:本小题主要考查函数单调性的应用、函数奇偶性的应用、不等式的解法等基础知识,考查运算求解能力,考查化归与转化思想.属于基础题.

 )≠f(
)≠f( ),f(-
),f(- )≠-f(
)≠-f( ),故f(x)为非奇非偶函数;
),故f(x)为非奇非偶函数; )=[
)=[ [
[ ]]=[
]]=[ •1]=[
•1]=[ ]=1,
]=1, )=[-
)=[- [-
[- ]]=[-
]]=[- •(-2)]=[3]=3,
•(-2)]=[3]=3, )≠f(
)≠f( ),f(-
),f(- )≠-f(
)≠-f( ),故f(x)为非奇非偶函数.(4分)
),故f(x)为非奇非偶函数.(4分)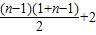 =
=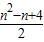 (14分)
(14分)

 阅读快车系列答案
阅读快车系列答案