
【题目】在△ABC中,∠ABC= ![]() ,边BC在平面α内,顶点A在平面α外,直线AB与平面α所成角为θ.若平面ABC与平面α所成的二面角为
,边BC在平面α内,顶点A在平面α外,直线AB与平面α所成角为θ.若平面ABC与平面α所成的二面角为 ![]() ,则sinθ= .
,则sinθ= . 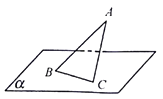
科目:高中数学 来源: 题型:
【题目】已知幂函数f(x)=![]() ,其中2<m<2,m∈Z,满足:
,其中2<m<2,m∈Z,满足:
(1)f(x)是区间(0,+∞)上的增函数;
(2)对任意的x∈R,都有f(x) +f(x)=0.
求同时满足条件(1)、(2)的幂函数f(x)的解析式,并求x∈[0,3]时,f(x)的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆M:(x﹣1)2+y2= ![]() ,椭圆C:
,椭圆C: ![]() +y2=1,若直线l与椭圆交于A,B两点,与圆M相切于点P,且P为AB的中点,则这样的直线l有( )
+y2=1,若直线l与椭圆交于A,B两点,与圆M相切于点P,且P为AB的中点,则这样的直线l有( )
A.2条
B.3条
C.4条
D.6条
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知PA⊥平面ABCD,且四边形ABCD为矩形,M、N分别是AB、PC的中点.

(1)求证:MN⊥CD;
(2)若∠PDA=45°,求证:MN⊥平面PCD.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,P是直线x=4上一动点,以P为圆心的圆Γ经定点B(1,0),直线l是圆Γ在点B处的切线,过A(﹣1,0)作圆Γ的两条切线分别与l交于E,F两点. 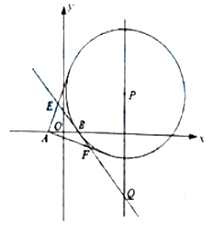
(1)求证:|EA|+|EB|为定值;
(2)证明:设直线l交直线x=4于点Q,证明:|EB||FQ|=|BF|EQ|.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知幂函数f(x)=xa的图象经过点![]() .
.
(1)求函数f(x)的解析式,并判断奇偶性;
(2)判断函数f(x)在(﹣![]() ,0)上的单调性,并用单调性定义证明.
,0)上的单调性,并用单调性定义证明.
(3)作出函数f(x)在定义域内的大致图象(不必写出作图过程).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x3﹣3x2﹣9x+1(x∈R).
(1)求函数f(x)的单调区间.
(2)若f(x)﹣2a+1≥0对x∈[﹣2,4]恒成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市出租车的现行计价标准是:路程在2 km以内(含2 km)按起步价8元收取,超过2 km后的路程按1.9 元/km收取,但超过10 km后的路程需加收50%的返空费(即单价为1.9×(1+50%)=2.85(元/km)).
(1)将某乘客搭乘一次出租车的费用f(x)(单位:元)表示为行程x(0<x≤60,单位:km)的分段函数;
(2)某乘客的行程为16 km,他准备先乘一辆出租车行驶8 km后,再换乘另一辆出租车完成余下行程,请问:他这样做是否比只乘一辆出租车完成全部行程更省钱?
(现实中要计等待时间且最终付费取整数,本题在计算时都不予考虑)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com