
ΓΨΧβΡΩΓΩΈΣΙα≥Ι¬δ ΒΒ≥÷–―κ»ΪΟφΫ®…η–ΓΩΒ…γΜαΒΡ’Ϋ¬‘≤Ω πΘ§Ρ≥ΤΕάßΒΊ«χΒΡΙψ¥σΒ≥‘±Η…≤Ω…ν»κ≈©¥εΜΐΦΪΩΣ’ΙΓΑΨΪΉΦΖωΤΕΓ±ΙΛΉς.Ψ≠ΙΐΕύΡξΒΡΨΪ–ΡΑοΖωΘ§ΫΊ÷Ν2018ΡξΒΉΘ§Α¥’’≈©¥εΦ“ΆΞ»ΥΨυΡξ¥Ω ’»κ8000‘ΣΒΡ–ΓΩΒ±ξΉΦΘ§ΗΟΒΊ«χΫω Θ≤ΩΖ÷Φ“ΆΞ…–Έ¥ Βœ÷–ΓΩΒ.œ÷¥”’β–©…–Έ¥ Βœ÷–ΓΩΒΒΡΦ“ΆΞ÷–ΥφΜζ≥ι»Γ50ΜßΘ§ΒΟΒΫ’β50ΜßΦ“ΆΞ2018ΡξΒΡΦ“ΆΞ»ΥΨυΡξ¥Ω ’»κΒΡΤΒ¬ Ζ÷≤Φ÷±ΖΫΆΦΘ§»γΆΦ.
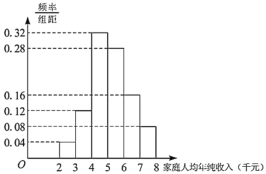
ΉΔΘΚ‘ΎΤΒ¬ Ζ÷≤Φ÷±ΖΫΆΦ÷–Θ§Ά§“ΜΉι ΐΨί”ΟΗΟ«χΦδΒΡ÷–Βψ÷ΒΉς¥ζ±μ.
Θ®1Θ©ΙάΦΤΗΟΒΊ«χ…–Έ¥ Βœ÷–ΓΩΒΒΡΦ“ΆΞ2018ΡξΦ“ΆΞ»ΥΨυΡξ¥Ω ’»κΒΡΤΫΨυ÷ΒΘΜ
Θ®2Θ©2019Ρξ7‘¬Θ§ΈΣΙάΦΤΗΟΒΊΡήΖώ‘Ύ2020Ρξ»ΪΟφ Βœ÷–ΓΩΒΘ§ ’Φ·ΝΥΒ±ΒΊΉνΤΕάßΒΡ“ΜΜßΦ“ΆΞ2019Ρξ1÷Ν6‘¬ΒΡ»ΥΨυ‘¬¥Ω ’»κΒΡ ΐΨίΘ§Ής≥ω…ΔΒψΆΦ»γœ¬.
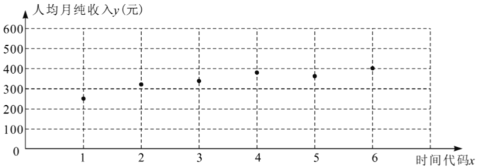
ΗυΨίœύΙΊ–‘Ζ÷ΈωΘ§ΖΔœ÷ΤδΦ“ΆΞ»ΥΨυ‘¬¥Ω ’»κ![]() ”κ ±Φδ¥ζ¬κ
”κ ±Φδ¥ζ¬κ![]() ÷°ΦδΨΏ”–Ϋœ«ΩΒΡœΏ–‘œύΙΊΙΊœΒΘ®Φ«2019Ρξ1‘¬ΓΔ2‘¬Γ≠Γ≠Ζ÷±πΈΣ
÷°ΦδΨΏ”–Ϋœ«ΩΒΡœΏ–‘œύΙΊΙΊœΒΘ®Φ«2019Ρξ1‘¬ΓΔ2‘¬Γ≠Γ≠Ζ÷±πΈΣ![]() Θ§
Θ§![]() Θ§Γ≠Θ§“ά¥ΥάύΆΤΘ©. ‘‘Λ≤βΗΟΦ“ΆΞΡήΖώ‘Ύ2020Ρξ Βœ÷–ΓΩΒ…ζΜν.
Θ§Γ≠Θ§“ά¥ΥάύΆΤΘ©. ‘‘Λ≤βΗΟΦ“ΆΞΡήΖώ‘Ύ2020Ρξ Βœ÷–ΓΩΒ…ζΜν.
≤ΈΩΦ ΐΨίΘΚ![]() Θ§
Θ§![]() .
.
≤ΈΩΦΙΪ ΫΘΚœΏ–‘ΜΊΙιΖΫ≥Χ![]() ÷–Θ§
÷–Θ§ Θ§
Θ§![]() .
.
ΓΨ¥πΑΗΓΩΘ®1Θ©![]() Θ®‘ΣΘ©Θ®2Θ©‘Λ≤βΗΟΦ“ΆΞΡή‘Ύ2020Ρξ Βœ÷–ΓΩΒ…ζΜν
Θ®‘ΣΘ©Θ®2Θ©‘Λ≤βΗΟΦ“ΆΞΡή‘Ύ2020Ρξ Βœ÷–ΓΩΒ…ζΜν
ΓΨΫβΈωΓΩ
Θ®1Θ©÷±Ϋ”ΦΤΥψΒΟΒΫ¥πΑΗ.
Θ®2Θ©ΦΤΥψ![]() Θ§
Θ§![]() Θ§ΒΟΒΫΜΊΙιΖΫ≥Χ
Θ§ΒΟΒΫΜΊΙιΖΫ≥Χ![]() Θ§»Γ
Θ§»Γ![]() Θ§
Θ§![]() Θ§ΦΤΥψΒΟΒΫ
Θ§ΦΤΥψΒΟΒΫ![]() Θ§
Θ§![]() Θ§‘ΌΗυΨίΒ»≤ν ΐΝ–ΙΪ ΫΦΤΥψΒΟΒΫ¥πΑΗ.
Θ§‘ΌΗυΨίΒ»≤ν ΐΝ–ΙΪ ΫΦΤΥψΒΟΒΫ¥πΑΗ.
Θ®1Θ©”…ΤΒ¬ Ζ÷≤Φ÷±ΖΫΆΦΩ…ΒΟ2018Ρξ’β50ΜßΦ“ΆΞ»ΥΨυΡξ¥Ω ’»κΒΡΤΫΨυ÷ΒΈΣ
![]()
![]() Θ®‘ΣΘ©.
Θ®‘ΣΘ©.
Θ®2Θ©“άΧβ“βΘ§Ω…ΒΟΘΚ![]() Θ§Ι
Θ§Ι ![]() Θ§
Θ§
Υυ“‘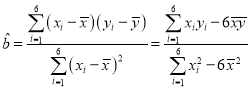
![]()
![]() .
.![]() Θ§
Θ§
Υυ“‘![]() ΙΊ”Ύ
ΙΊ”Ύ![]() ΒΡœΏ–‘ΜΊΙιΖΫ≥ΧΈΣ
ΒΡœΏ–‘ΜΊΙιΖΫ≥ΧΈΣ![]() .
.
Νν![]() Θ§ΒΟ2020Ρξ1‘¬ΗΟΦ“ΆΞ»ΥΨυ‘¬¥Ω ’»κΈΣ
Θ§ΒΟ2020Ρξ1‘¬ΗΟΦ“ΆΞ»ΥΨυ‘¬¥Ω ’»κΈΣ![]() Θ®‘ΣΘ©Θ§
Θ®‘ΣΘ©Θ§
Νν![]() Θ§ΒΟ2020Ρξ12‘¬ΗΟΦ“ΆΞ»ΥΨυ‘¬¥Ω ’»κΈΣ
Θ§ΒΟ2020Ρξ12‘¬ΗΟΦ“ΆΞ»ΥΨυ‘¬¥Ω ’»κΈΣ![]() Θ®‘ΣΘ©Θ§
Θ®‘ΣΘ©Θ§
”…Χβ“β÷ΣΘ§ΗΟΦ“ΆΞΒΡ»ΥΨυ‘¬¥Ω ’»κΒΡΙάΦΤ÷Β≥…Β»≤ν ΐΝ–Θ§
Υυ“‘Θ§2020ΡξΗΟΦ“ΆΞ»ΥΨυΡξ¥Ω ’»κΒΡΙάΦΤ÷ΒΈΣ![]() Θ§
Θ§
Ήέ…œΘ§‘Λ≤βΗΟΦ“ΆΞΡή‘Ύ2020Ρξ Βœ÷–ΓΩΒ…ζΜν.



| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩœ¬±μ «Ρ≥ΙΪΥΨ![]() Ρξ
Ρξ![]() ‘¬Ζί―–ΖΔΖ―”Ο
‘¬Ζί―–ΖΔΖ―”Ο![]() Θ®ΑΌΆρ‘ΣΘ©ΚΆ≤ζΤΖœζΝΩ
Θ®ΑΌΆρ‘ΣΘ©ΚΆ≤ζΤΖœζΝΩ![]() Θ®ΆρΧ®Θ©ΒΡΨΏΧε ΐΨίΘΚ
Θ®ΆρΧ®Θ©ΒΡΨΏΧε ΐΨίΘΚ
‘¬ Ζί |
|
|
|
|
|
|
|
|
―–ΖΔΖ―”ΟΘ®ΑΌΆρ‘ΣΘ© |
|
|
|
|
|
|
|
|
≤ζΤΖœζΝΩΘ®ΆρΧ®Θ© |
|
|
|
|
|
|
|
|
Θ®1Θ©ΗυΨί ΐΨίΩ…÷Σ![]() ”κ
”κ![]() ÷°Φδ¥φ‘ΎœΏ–‘œύΙΊΙΊœΒΘ§”ΟœΏ–‘œύΙΊœΒ ΐΥΒΟς
÷°Φδ¥φ‘ΎœΏ–‘œύΙΊΙΊœΒΘ§”ΟœΏ–‘œύΙΊœΒ ΐΥΒΟς![]() ”κ
”κ![]() ÷°ΦδΒΡœύΙΊ–‘«Ω»θ≥ΧΕ»
÷°ΦδΒΡœύΙΊ–‘«Ω»θ≥ΧΕ»
Θ®2Θ©«σ≥ω![]() ”κ
”κ![]() ΒΡœΏ–‘ΜΊΙιΖΫ≥ΧΘ®œΒ ΐΨΪ»ΖΒΫ
ΒΡœΏ–‘ΜΊΙιΖΫ≥ΧΘ®œΒ ΐΨΪ»ΖΒΫ![]() Θ©Θ§≤ΔΙάΦΤΒ±―–ΖΔΖ―”ΟΈΣ
Θ©Θ§≤ΔΙάΦΤΒ±―–ΖΔΖ―”ΟΈΣ![]() Θ®ΑΌΆρ‘ΣΘ© ±ΗΟ≤ζΤΖΒΡœζΝΩ.
Θ®ΑΌΆρ‘ΣΘ© ±ΗΟ≤ζΤΖΒΡœζΝΩ.
≤ΈΩΦ ΐΨίΘΚ![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]()
≤Έ’’ΙΪ ΫΘΚœύΙΊœΒ ΐ Θ§ΤδΜΊΙι÷±œΏ
Θ§ΤδΜΊΙι÷±œΏ![]() ÷–ΒΡ
÷–ΒΡ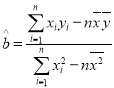
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣΆ÷‘≤![]() ΘΚ
ΘΚ![]() ΒΡΉσΫΙΒψΈΣ
ΒΡΉσΫΙΒψΈΣ![]() .
.
Θ®1Θ©«σΆ÷‘≤![]() ΒΡάκ–Ρ¬ ΘΜ
ΒΡάκ–Ρ¬ ΘΜ
Θ®2Θ©…η![]() ΈΣΉχ±ξ‘≠ΒψΘ§
ΈΣΉχ±ξ‘≠ΒψΘ§![]() ΈΣ÷±œΏ
ΈΣ÷±œΏ![]() …œ“ΜΒψΘ§Ιΐ
…œ“ΜΒψΘ§Ιΐ![]() Ής
Ής![]() ΒΡ¥ΙœΏΫΜΆ÷‘≤”Ύ
ΒΡ¥ΙœΏΫΜΆ÷‘≤”Ύ![]() Θ§
Θ§![]() .Β±ΥΡ±Ώ–Έ
.Β±ΥΡ±Ώ–Έ![]() «ΤΫ––ΥΡ±Ώ–Έ ±Θ§«σΥΡ±Ώ–Έ
«ΤΫ––ΥΡ±Ώ–Έ ±Θ§«σΥΡ±Ώ–Έ![]() ΒΡΟφΜΐ.
ΒΡΟφΜΐ.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΒ¬Ιζ÷χΟϊ ΐ―ßΦ“Β“άϊΩΥάΉ‘Ύ ΐ―ßΝλ”ρ≥…ΨΆœ‘÷χΘ§“‘ΤδΟϊΟϋΟϊΒΡΚ· ΐ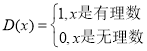 Θ§±Μ≥ΤΈΣΒ“άϊΩΥάΉΚ· ΐΘ°“‘œ¬ΥΒΖ®’ΐ»ΖΒΡ «Θ® Θ©Θ°
Θ§±Μ≥ΤΈΣΒ“άϊΩΥάΉΚ· ΐΘ°“‘œ¬ΥΒΖ®’ΐ»ΖΒΡ «Θ® Θ©Θ°
A.![]() ΒΡ÷Β”ρ «
ΒΡ÷Β”ρ «![]()
B.![]() Θ§ΕΦ”–
Θ§ΕΦ”–![]()
C.¥φ‘ΎΖ«Νψ Β ΐ![]() Θ§ ΙΒΟ
Θ§ ΙΒΟ![]()
D.Ε‘»Έ“β![]() Θ§ΕΦ”–
Θ§ΕΦ”–![]()
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣΚ· ΐ![]() Θ§
Θ§![]() Θ§
Θ§![]() .Κ· ΐ
.Κ· ΐ![]() ΒΡΒΦΚ· ΐ
ΒΡΒΦΚ· ΐ![]() ‘Ύ
‘Ύ![]() …œ¥φ‘ΎΝψΒψ.
…œ¥φ‘ΎΝψΒψ.
![]() «σ Β ΐ
«σ Β ΐ![]() ΒΡ»Γ÷ΒΖΕΈßΘΜ
ΒΡ»Γ÷ΒΖΕΈßΘΜ
![]() »τ¥φ‘Ύ Β ΐ
»τ¥φ‘Ύ Β ΐ![]() Θ§Β±
Θ§Β±![]() ±Θ§Κ· ΐ
±Θ§Κ· ΐ![]() ‘Ύ
‘Ύ![]() ±»ΓΒΟΉν¥σ÷ΒΘ§«σ’ΐ Β ΐ
±»ΓΒΟΉν¥σ÷ΒΘ§«σ’ΐ Β ΐ![]() ΒΡΉν¥σ÷ΒΘΜ
ΒΡΉν¥σ÷ΒΘΜ
![]() »τ÷±œΏ
»τ÷±œΏ![]() ”κ«ζœΏ
”κ«ζœΏ![]() ΚΆ
ΚΆ![]() ΕΦœύ«–Θ§«“
ΕΦœύ«–Θ§«“![]() ‘Ύ
‘Ύ![]() ÷α…œΒΡΫΊΨύΈΣ
÷α…œΒΡΫΊΨύΈΣ![]() Θ§«σ Β ΐ
Θ§«σ Β ΐ![]() ΒΡ÷Β.
ΒΡ÷Β.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷Σ≈ΉΈοœΏ![]() ΒΡΉΦœΏ”κx÷αΒΡΫΜΒψΈΣHΘ§ΒψFΈΣ≈ΉΈοœΏΒΡΫΙΒψΘ§ΒψP‘Ύ≈ΉΈοœΏ…œ«“
ΒΡΉΦœΏ”κx÷αΒΡΫΜΒψΈΣHΘ§ΒψFΈΣ≈ΉΈοœΏΒΡΫΙΒψΘ§ΒψP‘Ύ≈ΉΈοœΏ…œ«“![]() Θ§Β±kΉν¥σ ±Θ§ΒψP«ΓΚΟ‘Ύ“‘HΘ§FΈΣΫΙΒψΒΡΥΪ«ζœΏ…œΘ§‘ρkΒΡΉν¥σ÷ΒΈΣ_____Θ§¥Υ ±ΗΟΥΪ«ζœΏΒΡάκ–Ρ¬ ΈΣ_____Θ°
Θ§Β±kΉν¥σ ±Θ§ΒψP«ΓΚΟ‘Ύ“‘HΘ§FΈΣΫΙΒψΒΡΥΪ«ζœΏ…œΘ§‘ρkΒΡΉν¥σ÷ΒΈΣ_____Θ§¥Υ ±ΗΟΥΪ«ζœΏΒΡάκ–Ρ¬ ΈΣ_____Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘Ύ÷±Ϋ«Χί–Έ![]() ÷–Θ§
÷–Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]() «
«![]() …œ“ΜΒψΘ§
…œ“ΜΒψΘ§![]() Θ§œ÷―Ί
Θ§œ÷―Ί![]() ΫΪ
ΫΪ![]() ’έΤπΒΫ
’έΤπΒΫ![]() ΒΡΈΜ÷ΟΘ§≤Δ Ι
ΒΡΈΜ÷ΟΘ§≤Δ Ι![]() ΤΫΟφ
ΤΫΟφ![]() Θ§Βψ
Θ§Βψ![]() ‘Ύ
‘Ύ![]() ±Ώ…œΘ§«“¬ζΉψ
±Ώ…œΘ§«“¬ζΉψ![]() .
.
Θ®1Θ©÷ΛΟςΘΚ![]() ΤΫΟφ
ΤΫΟφ![]() ΘΜ
ΘΜ
Θ®2Θ©»τ![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§«σΕΰΟφΫ«
Θ§«σΕΰΟφΫ«![]() ΒΡ¥σ–Γ.
ΒΡ¥σ–Γ.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ―Γ–ό4ΓΣ4ΘΚΉχ±ξœΒ”κ≤Έ ΐΖΫ≥Χ
ΤΫΟφ÷±Ϋ«Ήχ±ξœΒxOy÷–Θ§«ζœΏCΘΚ![]() Θ°÷±œΏlΨ≠ΙΐΒψPΘ®mΘ§0Θ©Θ§«“«ψ–±Ϋ«ΈΣ
Θ°÷±œΏlΨ≠ΙΐΒψPΘ®mΘ§0Θ©Θ§«“«ψ–±Ϋ«ΈΣ![]() Θ°OΈΣΦΪΒψΘ§“‘x÷α’ΐΑκ÷αΈΣΦΪ÷αΘ§Ϋ®ΝΔΦΪΉχ±ξœΒΘ°
Θ°OΈΣΦΪΒψΘ§“‘x÷α’ΐΑκ÷αΈΣΦΪ÷αΘ§Ϋ®ΝΔΦΪΉχ±ξœΒΘ°
Θ®ΔώΘ©–¥≥ω«ζœΏCΒΡΦΪΉχ±ξΖΫ≥Χ”κ÷±œΏlΒΡ≤Έ ΐΖΫ≥ΧΘΜ
Θ®ΔρΘ©»τ÷±œΏl”κ«ζœΏCœύΫΜ”ΎAΘ§BΝΫΒψΘ§«“ΘϋPAΘϋΓΛΘϋPBΘϋΘΫ1Θ§«σ Β ΐmΒΡ÷ΒΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
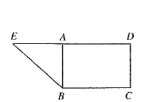
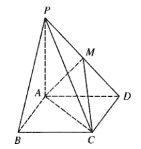
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘ΎΥΡάβΉΕP©¹ABCD÷–Θ§ΒΉΟφABCD «’ΐΖΫ–ΈΘ§PAΘΫABΘΫ1Θ§![]()

Θ®1Θ©÷ΛΟςΘΚBDΓΆΤΫΟφPACΘΜ
Θ®2Θ©»τE «PCΒΡ÷–ΒψΘ§F «άβPD…œ“ΜΒψΘ§«“BEΓΈΤΫΟφACFΘ§«σΕΰΟφΫ«F©¹AC©¹DΒΡ”ύœ“÷ΒΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΑΌΕ»÷¬–≈ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com