
【题目】如图,![]() 是通过某城市开发区中心O的两条南北和东西走向的街道,连结M,N两地之间的铁路线是圆心在
是通过某城市开发区中心O的两条南北和东西走向的街道,连结M,N两地之间的铁路线是圆心在![]() 上的一段圆弧,若点M在点O正北方向3公里;点N到的
上的一段圆弧,若点M在点O正北方向3公里;点N到的![]() 距离分别为4公里和5公里.
距离分别为4公里和5公里.
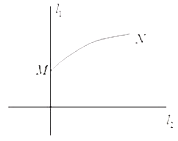
(1)建立适当的坐标系,求铁路线所在圆弧的方程;
(2)若该城市的某中学拟在点O的正东方向选址建分校,考虑环境问题,要求校址到点O的距离大于4公里,并且铁路上任意一点到校址的距离不能小于![]() 公里,求该校址距点O的最短距离(注:校址视为一个点)
公里,求该校址距点O的最短距离(注:校址视为一个点)
科目:高中数学 来源: 题型:
【题目】2019年全国“两会”,即中华人民共和国第十三届全国人大二次会议和中国人民政治协商会议第十三届全国委员会第二次会议,分别于2019年3月5日和3月3日在北京召开.为了了解哪些人更关注“两会”,某机构随机抽取了年龄在15~75岁之间的200人进行调查,并按年龄绘制的频率分布直方图如下图所示,把年龄落在区间[15,35)和[35,75]内的人分别称为“青少年人”和“中老年人”.经统计“青少年人”和“中老年人”的人数之比为19:21.其中“青少年人”中有40人关注“两会”,“中老年人”中关注“两会”和不关注“两会”的人数之比是2:1.
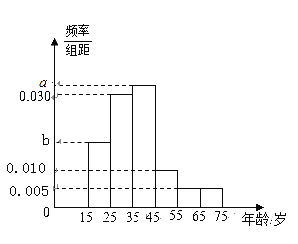
(Ⅰ)求图中![]() 的值;
的值;
(Ⅱ)现采用分层抽样在[25,35)和[45,55)中随机抽取8名代表,从8人中任选2人,求2人中至少有1个是“中老年人”的概率是多少?
(Ⅲ)根据已知条件,完成下面的2×2列联表,并根据此统计结果判断:能否有99.9%的把握认为“中老年人”比“青少年人”更加关注“两会”?
关注 | 不关注 | 合计 | |
青少年人 | |||
中老年人 | |||
合计 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 的圆心在射线
的圆心在射线![]() 上,截直线
上,截直线![]() 所得的弦长为6,且与直线
所得的弦长为6,且与直线![]() 相切.
相切.
(1)求圆![]() 的方程;
的方程;
(2)已知点![]() ,在直线
,在直线![]() 上是否存在点
上是否存在点![]() (异于点
(异于点![]() ),使得对圆
),使得对圆![]() 上的任一点
上的任一点![]() ,都有
,都有![]() 为定值
为定值![]() ?若存在,请求出点
?若存在,请求出点![]() 的坐标及
的坐标及![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】椭圆b2x2+a2y2=a2b2(a>b>0)的两个焦点分别是F1、F2,等边三角形的边AF1、AF2与该椭圆分别相交于B、C两点,且2|BC|=|F1F2|,则该椭圆的离心率等于( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知动圆C过定点F(2,0),且与直线x=-2相切,圆心C的轨迹为E,
(1)求圆心C的轨迹E的方程;
(2)若直线l交E与P,Q两点,且线段PQ的中心点坐标(1,1),求|PQ|.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正方形![]() 的边长为2,
的边长为2,![]() ,
,![]() 分别为
分别为![]() 的中点,
的中点,![]() 与
与![]() 交于点
交于点![]() ,将
,将![]() 沿
沿![]() 折起到
折起到![]() 的位置,使平面
的位置,使平面![]() 平面
平面![]() .
.
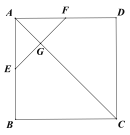

(Ⅰ)求证:平面![]() 平面
平面![]() ;
;
(Ⅱ)求二面角![]() 的余弦值;
的余弦值;
(Ⅲ)判断线段![]() 上是否存在点
上是否存在点![]() ,使
,使![]() 平面
平面![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com