
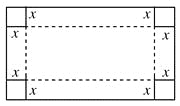
【题目】今有一长2米宽1米的矩形铁皮,如图,在四个角上分别截去一个边长为x米的正方形后,沿虚线折起可做成一个无盖的长方体形水箱(接口连接问题不考虑).
(Ⅰ)求水箱容积的表达式![]() ,并指出函数
,并指出函数![]() 的定义域;
的定义域;
(Ⅱ)若要使水箱容积不大于![]() 立方米的同时,又使得底面积最大,求x的值.
立方米的同时,又使得底面积最大,求x的值.
科目:高中数学 来源: 题型:
【题目】将函数![]() 的图象向右平移
的图象向右平移![]() 个单位后得到函数
个单位后得到函数![]() 的图象,则( )
的图象,则( )
A. ![]() 图象关于直线
图象关于直线![]() 对称 B.
对称 B. ![]() 图象关于点
图象关于点![]() 中心对称
中心对称
C. ![]() 在区间
在区间![]() 单调递增 D.
单调递增 D. ![]() 在区间
在区间![]() 上单调递减
上单调递减
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】抛掷一个质地均匀的骰子的试验,事件A表示“小于5的偶数点出现”,事件B表示“不小于5的点数出现”,则一次试验中,事件A或事件B至少有一个发生的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】 稿酬所得以个人每次取得的收入,定额或定率减除规定费用后的余额为应纳税所得额,每次收入不超过4000元,定额减除费用800元;每次收入在4000元以上的,定率减除20%的费用.适用20%的比例税率,并按规定对应纳税额减征30%,计算公式为:
(1)每次收入不超过4000元的:应纳税额=(每次收入额-800)×20%×(1-30%)
(2)每次收入在4000元以上的:应纳税额=每次收入额×(1-20%)×20%×(1-30%).已知某人出版一份书稿,共纳税280元,这个人应得稿费(扣税前)为 元.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ex﹣1+alnx.(e为自然对数的底数),λ=min{a+2,5}.(min{a,b}表示a,b中较小的数.)
(1)当a=0时,设g(x)=f(x)﹣x,求函数g(x)在[![]() ,
,![]() ]上的最值;
]上的最值;
(2)当x![]() 1时,证明:f(x)+x2
1时,证明:f(x)+x2![]() λ(x﹣1)+2.
λ(x﹣1)+2.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】射击测试有两种方案,方案1:先在甲靶射击一次,以后都在乙靶射击;方案2:始终在乙靶射击,某射手命中甲靶的概率为![]() ,命中一次得3分;命中乙靶的概率为
,命中一次得3分;命中乙靶的概率为![]() ,命中一次得2分,若没有命中则得0分,用随机变量
,命中一次得2分,若没有命中则得0分,用随机变量![]() 表示该射手一次测试累计得分,如果
表示该射手一次测试累计得分,如果![]() 的值不低于3分就认为通过测试,立即停止射击;否则继续射击,但一次测试最多打靶3次,每次射击的结果相互独立。
的值不低于3分就认为通过测试,立即停止射击;否则继续射击,但一次测试最多打靶3次,每次射击的结果相互独立。
(1)如果该射手选择方案1,求其测试结束后所得分![]() 的分布列和数学期望E
的分布列和数学期望E![]() ;
;
(2)该射手选择哪种方案通过测试的可能性大?请说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 是函数
是函数![]() 定义域的一个子集,若存在
定义域的一个子集,若存在![]() ,使得
,使得![]() 成立,则称
成立,则称![]() 是
是![]() 的一个“准不动点”,也称
的一个“准不动点”,也称![]() 在区间
在区间![]() 上存在准不动点,已知
上存在准不动点,已知![]() ,
,![]() .
.
(1)若![]() ,求函数
,求函数![]() 的准不动点;
的准不动点;
(2)若函数![]() 在区间
在区间![]() 上存在准不动点,求实数
上存在准不动点,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com