
分析 (1)先求f(x)的定义域,再求导f′(x)=$\frac{1}{x}$-a-$\frac{1-a}{{x}^{2}}$=$\frac{-a{x}^{2}+x+a-1}{{x}^{2}}$,从而在定义域内判断导数的正负,以确定函数的单调性;
(2)(i)由题意,当a=$\frac{1}{4}$时,函数f(x)在(0,1)上是减函数,(1,2)上是增函数,从而可得fmin(x)=f(1)=-$\frac{1}{2}$,从而化为2bx≥x2+$\frac{9}{2}$在[1,3]上有解,从而求得;
(ii)不妨设1<x1<x2≤2,从而可得f(x2)+$\frac{λ}{{x}_{2}}$<f(x1)+$\frac{λ}{{x}_{1}}$,从而化为h(x)=f(x)+$\frac{λ}{x}$=lnx-$\frac{1}{4}$x+$\frac{3}{4x}$-1+$\frac{λ}{x}$在(1,2]是减函数,从而解得.
解答 解:(1)f(x)=lnx-ax+$\frac{1-a}{x}$-1的定义域为(0,+∞),
f′(x)=$\frac{1}{x}$-a-$\frac{1-a}{{x}^{2}}$=$\frac{-a{x}^{2}+x+a-1}{{x}^{2}}$,
令f′(x)=0可得x1=1,x2=$\frac{1}{a}$-1,x1-x2=$\frac{2a-1}{a}$,
①当0<a<$\frac{1}{2}$时,由f′(x)>0得1<x<$\frac{1}{a}$-1,
故函数f(x)在(1,$\frac{1}{a}$-1)上是增函数,
同理,函数f(x)在(0,1),($\frac{1}{a}$-1,+∞)上是减函数,
②当a=$\frac{1}{2}$时,f′(x)≤0恒成立,
故函数f(x)在(0,+∞)上是减函数,
③当$\frac{1}{2}$<a<1时,由f′(x)>0得$\frac{1}{a}$-1<x<1,
故函数f(x)在($\frac{1}{a}$-1,1)上是增函数,
同理,函数f(x)在(0,$\frac{1}{a}$-1),(1,+∞)上是减函数;
(2)(i)由题意,当a=$\frac{1}{4}$时,
函数f(x)在(0,1)上是减函数,(1,2)上是增函数,
所以fmin(x)=f(1)=-$\frac{1}{2}$,
所以只需存在x∈[1,3],使g(x)=x2-2bx+4≤-$\frac{1}{2}$,
即2bx≥x2+$\frac{9}{2}$在[1,3]上有解,
即2b≥x+$\frac{9}{2x}$在[1,3]上有解,
∵x+$\frac{9}{2x}$≥3$\sqrt{2}$,(当且仅当x=$\frac{9}{2x}$,即x=$\frac{3\sqrt{2}}{2}$时,等号成立);
故2b≥3$\sqrt{2}$,
故b≥$\frac{3\sqrt{2}}{2}$,
故实数b取值范围为[$\frac{3\sqrt{2}}{2}$,+∞);
(ii)不妨设1<x1<x2≤2,
∵函数f(x)在(1,2]上是增函数,函数y=$\frac{1}{x}$在(1,2]上是减函数,
∴|f(x1)-f(x2)|<λ|$\frac{1}{{x}_{1}}-\frac{1}{{x}_{2}}$|可化为
f(x2)-f(x1)<λ($\frac{1}{{x}_{1}}-\frac{1}{{x}_{2}}$),
即f(x2)+$\frac{λ}{{x}_{2}}$<f(x1)+$\frac{λ}{{x}_{1}}$,
设h(x)=f(x)+$\frac{λ}{x}$=lnx-$\frac{1}{4}$x+$\frac{3}{4x}$-1+$\frac{λ}{x}$,
故h(x)在(1,2]是减函数,
故h′(x)=$\frac{-\frac{1}{4}{x}^{2}+x+\frac{1}{4}-1-λ}{{x}^{2}}$≤0恒成立,
故λ≥-$\frac{1}{4}$x2+x-$\frac{3}{4}$=-$\frac{1}{4}$(x-2)2+$\frac{1}{4}$恒成立,
故λ≥$\frac{1}{4}$,
故λ的取值范围为[$\frac{1}{4}$,+∞).
点评 本题考查了导数的综合应用及基本不等式的应用,同时考查了函数的单调性的定义的应用.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $[{-\sqrt{6},\sqrt{6}}]$ | B. | $({-∞,-\frac{{\sqrt{6}}}{6}})$∪$({\frac{{\sqrt{6}}}{6},+∞})$ | C. | $({-∞,-\frac{{\sqrt{6}}}{6}}]$∪$[{\frac{{\sqrt{6}}}{6},+∞})$ | D. | 以上都不对 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
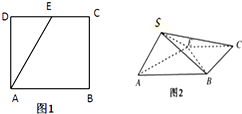 如图,点E为正方形ABCD边CD上异于点C,D的动点,将△ADE沿AE翻折成△SAE,使得平面SAE⊥平面ABCE,则下列三个说法中正确的个数是( )
如图,点E为正方形ABCD边CD上异于点C,D的动点,将△ADE沿AE翻折成△SAE,使得平面SAE⊥平面ABCE,则下列三个说法中正确的个数是( )| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com