
分析 (1)利用点到直线的距离公式,结合双曲线的方程,即可证明;
(2)设双曲线上一点P(x,y),若双曲线上一点P使得∠F1PF2为钝角,则$\overrightarrow{P{F}_{1}}$•$\overrightarrow{P{F}_{2}}$<0,由此列不等式解得P点横坐标的取值范围.
解答 (1)证明:设P(x,y),则
∵双曲线C的两条渐近线的方程为y=±$\frac{1}{2}$x,即x±2y=0
∴点P到双曲线C的两条渐近线的距离的乘积$\frac{|(x+2y)(x-2y)|}{5}$=$\frac{4}{5}$;
(2)解:设P(x,y),则$\overrightarrow{P{F}_{1}}$=(x+$\sqrt{5}$,y),$\overrightarrow{P{F}_{2}}$=(x-$\sqrt{5}$,y),
∵∠F1PF2为钝角,
∴$\overrightarrow{P{F}_{1}}$•$\overrightarrow{P{F}_{2}}$<0
∴cos∠F1PF2<0
∴(x+$\sqrt{5}$,y)•(x-$\sqrt{5}$,y)<0
即x2+y2-5<0
又$\frac{{x}^{2}}{4}-{y}^{2}$=1
∴$\frac{5}{4}$x2-6<0
解得x<-$\frac{2\sqrt{30}}{5}$或x>$\frac{2\sqrt{30}}{5}$.
点评 本题考查双曲线的标准方程及向量知识,解题时要能熟练的由双曲线定义和标准方程解焦点三角形问题.


科目:高中数学 来源: 题型:选择题
| A. | (1,-2,-3) | B. | (1,-2,3) | C. | (1,2,3) | D. | (-1,2,-3) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,点E在直角三角形ABC的斜边AB上,四边形CDEF为正方形,已知正方形CDEF的面积等于36.设AF=x,直角三角形ABC的面积S=f(x).
如图,点E在直角三角形ABC的斜边AB上,四边形CDEF为正方形,已知正方形CDEF的面积等于36.设AF=x,直角三角形ABC的面积S=f(x).查看答案和解析>>
科目:高中数学 来源: 题型:选择题
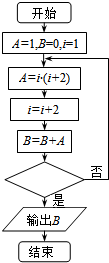 如图给出的是计算1×3+3×5+5×7+…+13×15的值的一个程序框图,其中判断框内应填入的条件不正确的是( )
如图给出的是计算1×3+3×5+5×7+…+13×15的值的一个程序框图,其中判断框内应填入的条件不正确的是( )| A. | i≥13? | B. | i>14? | C. | i≥14? | D. | i≥15? |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com