
【题目】已知函数f(x)是定义在R上的偶函数,且对任意x1 , x2∈(0,+∞)都有 ![]() <0(x1≠x2),若实数a满足f(log3a﹣1)+2f(
<0(x1≠x2),若实数a满足f(log3a﹣1)+2f( ![]() a)≥3f(1),则a的取值范围是( )
a)≥3f(1),则a的取值范围是( )
A.[ ![]() ,3]
,3]
B.[1,3]
C.(0, ![]() )
)
D.(0,3]
【答案】A
【解析】解:∵对任意x1 , x2∈(0,+∞)都有 ![]() <0(x1≠x2),
<0(x1≠x2),
∴此时函数为减函数,
则f(log3a﹣1)+2f( ![]() a)≥3f(1),等价为f(﹣log3a)+2f(﹣log3a)≥3f(1),
a)≥3f(1),等价为f(﹣log3a)+2f(﹣log3a)≥3f(1),
即3f(log3a)≥3f(1),
则f(log3a)≥f(1),
即f(|log3a|)≥f(1),
即|log3a|≤1,
则﹣1≤log3a≤1,
即 ![]() ≤a≤3,
≤a≤3,
故选:A
【考点精析】本题主要考查了函数奇偶性的性质和奇偶性与单调性的综合的相关知识点,需要掌握在公共定义域内,偶函数的加减乘除仍为偶函数;奇函数的加减仍为奇函数;奇数个奇函数的乘除认为奇函数;偶数个奇函数的乘除为偶函数;一奇一偶的乘积是奇函数;复合函数的奇偶性:一个为偶就为偶,两个为奇才为奇;奇函数在关于原点对称的区间上有相同的单调性;偶函数在关于原点对称的区间上有相反的单调性才能正确解答此题.


 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案科目:高中数学 来源: 题型:
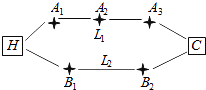
【题目】如图,李先生家住H小区,他工作在C科技园区,从家开车到公司上班路上有L1、L2两条路线,L1路线上有A1、A2、A3三个路口,各路口遇到红灯的概率均为 ![]() ;L2路线上有B1、B2两个路口,各路口遇到红灯的概率依次为
;L2路线上有B1、B2两个路口,各路口遇到红灯的概率依次为 ![]() ,
, ![]() .
. 
(1)若走L1路线,求最多遇到1次红灯的概率;
(2)若走L2路线,求遇到红灯次数X的数学期望;
(3)按照“平均遇到红灯次数最少”的要求,请你帮助李先生从上述两条路线中选择一条最好的上班路线,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是一几何体的平面展开图,其中ABCD为正方形,E,F分别为PA,PD的中点,
在此几何体中,给出下面四个结论:
①直线BE与直线CF异面; ②直线BE与直线AF异面;
③直线EF∥平面PBC; ④平面BCE⊥平面PAD.
其中正确的有( )
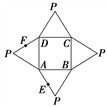
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱ABC﹣A1B1C1中,E,F分别是A1B,A1C的中点,点D在B1C1上,A1D⊥B1C.求证: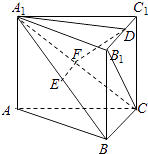
(1)EF∥平面ABC;
(2)平面A1FD⊥平面BB1C1C.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在长方形中,设一条对角线与其一顶点出发的两条边所成的角分别是α,β,则有cos2α+cos2β=1类比到空间,在长方体中,一条对角线与从其一顶点出发的三个面所成的角分别为α,β,γ,则有cos2α+cos2β+cos2γ= .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某普通高中为了了解学生的视力状况,随机抽查了100名高二年级学生和100名高三年级学生,对这些学生配戴眼镜的度数(简称:近视度数)进行统计,得到高二学生的频数分布表和高三学生频率分布直方图如下:
近视度数 | 0﹣100 | 100﹣200 | 200﹣300 | 300﹣400 | 400以上 |
学生频数 | 30 | 40 | 20 | 10 | 0 |
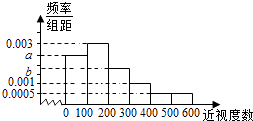
将近视程度由低到高分为4个等级:当近视度数在0﹣100时,称为不近视,记作0;当近视度数在100﹣200时,称为轻度近视,记作1;当近视度数在200﹣400时,称为中度近视,记作2;当近视度数在400以上时,称为高度近视,记作3.
(1)从该校任选1名高二学生,估计该生近视程度未达到中度及以上的概率;
(2)设a=0.0024,从该校任选1名高三学生,估计该生近视程度达到中度或中度以上的概率;
(3)把频率近似地看成概率,用随机变量X,Y分别表示高二、高三年级学生的近视程度,若EX=EY,求b.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在长方体ABCD﹣A1B1C1D1中,AB=BC=1,AA1=2,E为BB1中点. 
(1)证明:AC⊥D1E;
(2)求DE与平面AD1E所成角的正弦值;
(3)在棱AD上是否存在一点P,使得BP∥平面AD1E?若存在,求DP的长;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某连锁经营公司所属5个零售店某月的销售额和利润额资料如表:
商店名称 | A | B | C | D | E |
销售额x/千万元 | 3 | 5 | 6 | 7 | 9 |
利润额y/百万元 | 2 | 3 | 3 | 4 | 5 |
(1)画出销售额和利润额的散点图;
(2)若销售额和利润额具有相关关系,用最小二乘法计算利润额y对销售额x的回归直线方程;
(3)据(2)的结果估计当销售额为1亿元时的利润额.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com