(附加题)已知对于圆x2+(y-1)2=1上任意一点P(x,y)不等式x+y+m≥0恒成立,求实数m的取值范围.(满分10分,计入总分)
【答案】
分析:先设x=cosα,y-1=sinα,再把不等式x+y+m≥0恒成立转化为m≥-(x+y)恒成立,进而利用辅助角公式求-(x+y)的最小值即可得到结论.
解答:解:由题设:x=cosα,y-1=sinα,
则 x+y=cosα+sinα+1=
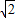
sin(α+
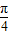
)+1∈[-
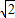
+1,
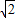
+1].
∵不等式x+y+m≥0恒成立
∴m≥-(x+y)恒成立;
因为-(x+y)的最大值为:
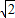
-1.
∴m≥
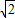
-1.
点评:本题主要考查函数的恒成立问题.解决问题的关键在于由不等式x+y+m≥0恒成立转化为m≥-(x+y)恒成立,进而求-(x+y)的最大值
