
【题目】如图,已知四边形ABCD是正方形,AE⊥平面ABCD,PD∥AE,PD=AD=2EA=2,G,F,H分别为BE,BP,PC的中点.
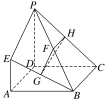
(1)求证:平面ABE⊥平面GHF;
(2)求直线GH与平面PBC所成的角θ的正弦值.
【答案】(1)证明见解析(2)![]()
【解析】
(1)通过证明BC⊥平面ABE,FH∥BC,证得FH⊥平面ABE,即可证得面面垂直;
(2)建立空间直角坐标系,利用向量方法求线面角的正弦值.
(1)由题:,AE⊥平面ABCD,BC![]() 平面ABCD,所以AE⊥BC,
平面ABCD,所以AE⊥BC,
四边形ABCD是正方形,AB⊥BC,AE与AB是平面ABE内两条相交直线,
所以BC⊥平面ABE,F,H分别为BP,PC的中点,所以FH∥BC,
所以FH⊥平面ABE,HF![]() 平面GHF,所以平面ABE⊥平面GHF;
平面GHF,所以平面ABE⊥平面GHF;
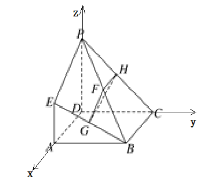
(2)由题可得:DA,DC,DP两两互相垂直,所以以D为原点,DA,DC,DP为x,y,z轴的正方向建立空间直角坐标系如图所示:
![]() ,
,
所以![]() ,设平面PBC的法向量
,设平面PBC的法向量![]() ,
,
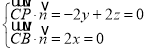 ,取
,取![]() 为平面PBC的一个法向量,
为平面PBC的一个法向量,
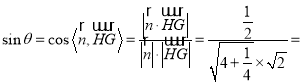
![]()
所以直线GH与平面PBC所成的角θ的正弦值![]() .
.


科目:高中数学 来源: 题型:
【题目】如图,在长方体![]() 中,
中,![]() 是
是![]() 的中点,点
的中点,点![]() 是
是![]() 上一点,
上一点,![]() ,
,![]() ,
,![]() .动点
.动点![]() 在上底面
在上底面![]() 上,且满足三棱锥
上,且满足三棱锥![]() 的体积等于1,则直线
的体积等于1,则直线![]() 与
与![]() 所成角的正切值的最大值为( )
所成角的正切值的最大值为( )

A.![]() B.
B.![]() C.
C.![]() D.2
D.2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市旅游管理部门为提升该市26个旅游景点的服务质量,对该市26个旅游景点的交通、安全、环保、卫生、管理五项指标进行评分,每项评分最低分0分,最高分100分,每个景点总分为这五项得分之和,根据考核评分结果,绘制交通得分与安全得分散点图、交通得分与景点总分散点图如下:
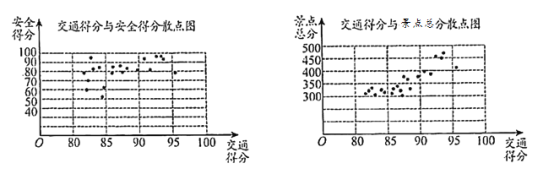
请根据图中所提供的信息,完成下列问题:
(I)若从交通得分前6名的景点中任取2个,求其安全得分都大于90分的概率;
(II)若从景点总分排名前6名的景点中任取3个,记安全得分不大于90分的景点个数为![]() ,求随机变量
,求随机变量![]() 的分布列和数学期望;
的分布列和数学期望;
(III)记该市26个景点的交通平均得分为![]() 安全平均得分为
安全平均得分为![]() ,写出
,写出![]() 和
和![]() 的大小关系?(只写出结果)
的大小关系?(只写出结果)
查看答案和解析>>
科目:高中数学 来源: 题型:
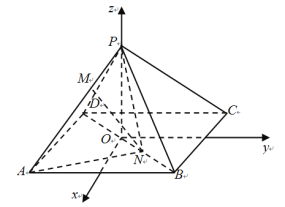
【题目】如图,在空间直角坐标系![]() 中,已知正四棱锥P-ABCD的所有棱长均为6,正方形ABCD的中心为坐标原点O,AD,BC平行于x轴,AB、CD平行于y轴,顶点P在z轴的正半轴上,点M、N分别在PA,BD上,且
中,已知正四棱锥P-ABCD的所有棱长均为6,正方形ABCD的中心为坐标原点O,AD,BC平行于x轴,AB、CD平行于y轴,顶点P在z轴的正半轴上,点M、N分别在PA,BD上,且![]() .
.
(1)若![]() ,求直线MN与PC所成角的大小;
,求直线MN与PC所成角的大小;
(2)若二面角A-PN-D的平面角的余弦值为![]() ,求λ的值.
,求λ的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
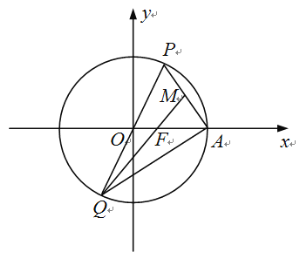
【题目】如图,在平面直角坐标系xOy中,椭圆![]() 的右焦点、右顶点分别为F,A,过原点的直线与椭圆C交于点P、Q(点P在第一象限内),连结PA,QF.若
的右焦点、右顶点分别为F,A,过原点的直线与椭圆C交于点P、Q(点P在第一象限内),连结PA,QF.若![]() ,
,![]() 的面积是
的面积是![]() 面积的3倍.
面积的3倍.
(1)求椭圆C的标准方程;
(2)已知M为线段PA的中点,连结QA,QM.
①求证:Q,F,M三点共线;
②记直线QP,QM,QA的斜率分别为![]() ,
,![]() ,
,![]() ,若
,若![]() ,求
,求![]() 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆![]() 的右焦点为
的右焦点为![]() ,以原点
,以原点![]() 为圆心,短半轴长为半径的圆恰好经过椭圆
为圆心,短半轴长为半径的圆恰好经过椭圆![]() 的两焦点,且该圆截直线
的两焦点,且该圆截直线![]() 所得的弦长为
所得的弦长为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)过定点![]() 的直线交椭圆
的直线交椭圆![]() 于两点
于两点![]() 、
、![]() ,椭圆上的点
,椭圆上的点![]() 满足
满足![]() ,试求
,试求![]() 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年底,武汉发生了新冠肺炎疫情,2020年初开始蔓延.党中央国务院面对“突发灾难”果断采取措施,举国上下,万众一心支援武汉,全国各地医疗队陆续增援湖北,纷纷投身疫情防控与救治病人之中.为了分担“抗疫英雄”的后顾之忧,某校教师志愿者开展“爱心辅导”活动,为抗疫前线医务工作者子女开展在线辅导.春节期间随机安排甲乙两位志愿者为一位初中生辅导功课共3次,每位志愿者至少辅导1次,每一次只有1位志愿者辅导,到甲恰好辅导两次的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以直角坐标系的原点为极点,![]() 轴的非负半轴为极轴建立极坐标系,曲线
轴的非负半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,直线
,直线![]() 的参数方程为
的参数方程为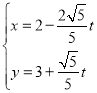 (
(![]() 为参数).
为参数).
(1)求曲线![]() 的参数方程与直线
的参数方程与直线![]() 的普通方程;
的普通方程;
(2)设点过![]() 为曲线
为曲线![]() 上的动点,点
上的动点,点![]() 和点
和点![]() 为直线
为直线![]() 上的点,且满足
上的点,且满足![]() 为等边三角形,求
为等边三角形,求![]() 边长的取值范围.
边长的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com