
【题目】对于实数a和b,定义运算“*”: ![]() ,设f(x)=(2x﹣1)*(x﹣1),且关于x的方程为f(x)=m(m∈R)恰有三个互不相等的实数根x1 , x2 , x3 , 则实数m的取值范围是;x1+x2+x3的取值范围是 .
,设f(x)=(2x﹣1)*(x﹣1),且关于x的方程为f(x)=m(m∈R)恰有三个互不相等的实数根x1 , x2 , x3 , 则实数m的取值范围是;x1+x2+x3的取值范围是 .
【答案】![]() ;
;![]()
【解析】解:∵ ![]() , ∴f(x)=(2x﹣1)*(x﹣1)=
, ∴f(x)=(2x﹣1)*(x﹣1)= ![]() ,
,
则当x=0时,函数取得极小值0,当x= ![]() 时,函数取得极大值
时,函数取得极大值 ![]()
故关于x的方程为f(x)=m(m∈R)恰有三个互不相等的实数根x1 , x2 , x3时,
实数m的取值范围是 ![]()
令f(x)= ![]() ,则x=
,则x= ![]() ,或x=
,或x= ![]()
不妨令x1<x2<x3时
则 ![]() <x1<0,x2+x3=1
<x1<0,x2+x3=1
∴x1+x2+x3的取值范围是 ![]()
故答案为: ![]() ,
, ![]()
由已知新定义,我们可以求出函数的解析式,进而分析出函数的两个极值点,进而求出x的方程为f(x)=m(m∈R)恰有三个互不相等的实数根时,实数m的取值范围,及三个实根之间的关系,进而求出x1+x2+x3的取值范围


科目:高中数学 来源: 题型:
【题目】如图,直四棱柱![]() 中,四边形
中,四边形![]() 为梯形,
为梯形, ![]() ,且
,且![]() .过
.过![]() 三点的平面记为
三点的平面记为![]() ,
, ![]() 与
与![]() 的交点为
的交点为![]() .
.
(I)证明: ![]() 为
为![]() 的中点;
的中点;
(II)求此四棱柱被平面![]() 所分成上下两部分的体积之比.
所分成上下两部分的体积之比.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设全集U=R,集合A={x|﹣1≤x<3},B={x|2x﹣4≤x﹣2}.
(1)求A∩(UB);
(2)若函数f(x)=lg(2x+a)的定义域为集合C,满足AC,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商场举行购物抽奖活动,抽奖箱中放有除编号不同外,其余均相同的20个小球,这20个小球编号的茎叶图如图所示,活动规则如下:从抽奖箱中随机抽取一球,若抽取的小球编号是十位数字为l的奇数,则为一等奖,奖金100元;若抽取的小球编号是十位数字为2的奇数,则为二等奖,奖金50元;若抽取的小球是其余编号则不中奖.现某顾客有放回的抽奖两次,两次抽奖相互独立. (I)求该顾客在两次抽奖中恰有一次中奖的概率;
(Ⅱ)记该顾客两次抽奖后的奖金之和为随机变量X,求X的分布列和数学期望.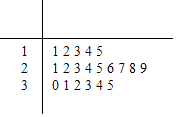
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂为了对新研发的产品进行合理定价,将该产品按事先拟定的价格进行试销,得到一组检测数据![]() ,如下表所示:
,如下表所示:
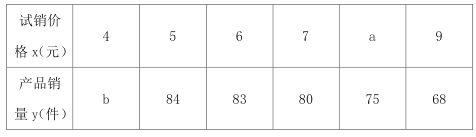
已知变量![]() 具有线性负相关关系,且
具有线性负相关关系,且![]() ,
, ![]() ,现有甲、乙、丙三位同学通过计算求得其回归直线方程分别为:甲
,现有甲、乙、丙三位同学通过计算求得其回归直线方程分别为:甲![]() ;乙
;乙![]() ;丙
;丙![]() ,其中有且仅有一位同学的计算结果是正确的.
,其中有且仅有一位同学的计算结果是正确的.
(1)试判断谁的计算结果正确?并求出![]() 的值;
的值;
(2)若由线性回归方程得到的估计数据与检测数据的误差不超过1,则该检测数据是“理想数据”,现从检测数据中随机抽取2个,求这两个检测数据均为“理想数据”的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线C1在平面直角坐标系中的参数方程为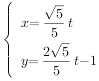 (t为参数),以坐标原点O为极点,x轴的非负半轴为极轴建立极坐标系,有曲线C2:ρ=2cosθ-4sinθ
(t为参数),以坐标原点O为极点,x轴的非负半轴为极轴建立极坐标系,有曲线C2:ρ=2cosθ-4sinθ
(1)将C1的方程化为普通方程,并求出C2的平面直角坐标方程
(2)求曲线C1和C2两交点之间的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是y=f(x)的导函数的图象,现有四种说法: 1)f(x)在(﹣2,1)上是增函数;
2)x=﹣1是f(x)的极小值点;
3)f(x)在(﹣1,2)上是增函数;
4)x=2是f(x)的极小值点;
以上说法正确的序号是 . 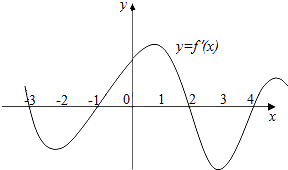
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2x,g(x)=x2+ax(其中a∈R).对于不相等的实数x1,x2,设m=![]() ,n=
,n=![]() .现有如下命题:
.现有如下命题:
①对于任意不相等的实数x1,x2,都有m>0;
②对于任意的a及任意不相等的实数x1,x2,都有n>0;
③对于任意的a,存在不相等的实数x1,x2,使得m=n;
④对于任意的a,存在不相等的实数x1,x2,使得m=-n.
其中的真命题有________(写出所有真命题的序号).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com