
【题目】某保险公司给年龄在![]() 岁的民众提供某种疾病的一年期医疗保险,现从
岁的民众提供某种疾病的一年期医疗保险,现从![]() 名参保人员中随机抽取
名参保人员中随机抽取![]() 名作为样本进行分析,按年龄段
名作为样本进行分析,按年龄段![]() 分成了五组,其频率分布直方图如下图所示;参保年龄与每人每年应交纳的保费如下表所示. 据统计,该公司每年为这一万名参保人员支出的各种费用为一百万元.
分成了五组,其频率分布直方图如下图所示;参保年龄与每人每年应交纳的保费如下表所示. 据统计,该公司每年为这一万名参保人员支出的各种费用为一百万元.
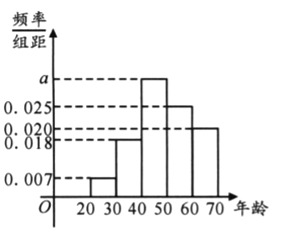
年龄 (单位:岁) |
|
|
|
|
|
保费 (单位:元) |
|
|
|
|
|
(1)用样本的频率分布估计总体分布,为使公司不亏本,求![]() 精确到整数时的最小值
精确到整数时的最小值![]() ;
;
(2)经调查,年龄在![]() 之间老人每
之间老人每![]() 人中有
人中有![]() 人患该项疾病(以此频率作为概率).该病的治疗费为
人患该项疾病(以此频率作为概率).该病的治疗费为![]() 元,如果参保,保险公司补贴治疗费
元,如果参保,保险公司补贴治疗费![]() 元.某老人年龄
元.某老人年龄![]() 岁,若购买该项保险(
岁,若购买该项保险(![]() 取
取![]() 中的
中的![]() ).针对此疾病所支付的费用为
).针对此疾病所支付的费用为![]() 元;若没有购买该项保险,针对此疾病所支付的费用为
元;若没有购买该项保险,针对此疾病所支付的费用为![]() 元.试比较
元.试比较![]() 和
和![]() 的期望值大小,并判断该老人购买此项保险是否划算?
的期望值大小,并判断该老人购买此项保险是否划算?
 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案科目:高中数学 来源: 题型:
【题目】已知圆![]() :
:![]() ,
,![]() :
:![]() ,动圆C与圆
,动圆C与圆![]() ,
,![]() 都相切,则动圆C的圆心轨迹E的方程为________________;斜率为
都相切,则动圆C的圆心轨迹E的方程为________________;斜率为![]() 的直线l与曲线E仅有三个公共点,依次为P,Q,R,则
的直线l与曲线E仅有三个公共点,依次为P,Q,R,则![]() 的值为________.
的值为________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P一ABCD中,AB=AD=2BC=2,BC∥AD,AB⊥AD,△PBD为正三角形.且PA=2![]() .
.
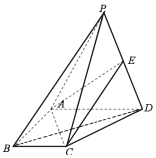
(1)证明:平面PAB⊥平面PBC;
(2)若点P到底面ABCD的距离为2,E是线段PD上一点,且PB∥平面ACE,求四面体A-CDE的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某高中数学建模兴趣小组的同学为了研究所在地区男高中生的身高与体重的关系,从若干个高中男学生中抽取了1000个样本,得到如下数据.
数据一:身高在![]() (单位:
(单位:![]() )的体重频数统计
)的体重频数统计
体重 ( |
|
|
|
|
|
|
|
|
人数 | 20 | 60 | 100 | 100 | 80 | 20 | 10 | 10 |
数据二:身高所在的区间含样本的个数及部分数据
身高 |
|
|
|
|
|
平均体重
| 45 | 53.6 | 60 | 75 |
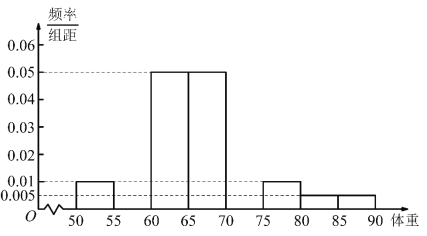
(1)依据数据一将上面男高中生身高在![]() (单位:
(单位:![]() )体重的频率分布直方图补充完整,并利用频率分布直方图估计身高在
)体重的频率分布直方图补充完整,并利用频率分布直方图估计身高在![]() (单位:
(单位:![]() )的中学生的平均体重;(保留小数点后一位)
)的中学生的平均体重;(保留小数点后一位)
(2)依据数据一、二,计算身高(取值为区间中点)和体重的相关系数约为0.99,能否用线性回归直线来刻画中学生身高与体重的相关关系,请说明理由;若能,求出该回归直线方程;
(3)说明残差平方和或相关指数![]() 与线性回归模型拟合效果之间关系.(只需写出结论,不需要计算)
与线性回归模型拟合效果之间关系.(只需写出结论,不需要计算)
参考公式: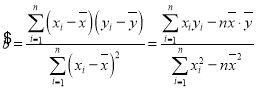 ,
,![]() .
.
参考数据:(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() ,
,![]() ,
,![]() ;(4)
;(4)![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
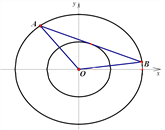
【题目】记焦点在同一条轴上且离心率相同的椭圆为“相似椭圆”.已知椭圆![]() ,以椭圆
,以椭圆![]() 的焦点为顶点作相似椭圆
的焦点为顶点作相似椭圆![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)设直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,且与椭圆
两点,且与椭圆![]() 仅有一个公共点,试判断
仅有一个公共点,试判断![]() 的面积是否为定值(
的面积是否为定值(![]() 为坐标原点)?若是,求出该定值;若不是,请说明理由.
为坐标原点)?若是,求出该定值;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将直角三角形![]() 沿斜边上的高
沿斜边上的高![]() 折成
折成![]() 的二面角,已知直角边
的二面角,已知直角边![]() ,那么下面说法正确的是_________.
,那么下面说法正确的是_________.
(1) 平面![]() 平面
平面![]() (2)四面体
(2)四面体![]() 的体积是
的体积是![]()
(3)二面角![]() 的正切值是
的正切值是![]() (4)
(4)![]() 与平面
与平面![]() 所成角的正弦值是
所成角的正弦值是![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com