【题目】已知函数f(x)＝
x3＋
x2－ax－a，x∈R，其中a＞0.
(1)求函数f(x)的单调区间；
(2)若函数f(x)在区间(－2,0)内恰有两个零点，求a的取值范围．
【答案】(1) 单调递增区间是(－∞，－1)，(a，＋∞)；单调递减区间是(－1，a)．(2)
【解析】(1)f′(x)＝x2＋(1－a)x－a＝(x＋1)(x－a)．
由f′(x)＝0，得x1＝－1，x2＝a＞0.
当x变化时，f′(x)，f(x)的变化情况如下表：
x | (－∞，－1) | －1 | (－1，a) | a | (a，＋∞) |
f′(x) | ＋ | 0 | － | 0 | ＋ |
f(x) |
| 极大值 |
| 极小值 |
|
故函数f(x)的单调递增区间是(－∞，－1)，(a，＋∞)；单调递减区间是(－1，a)．
(2)由(1)知f(x)在区间(－2，－1)内单调递增，在区间(－1，0)内单调递减，从而函数f(x)在区间(－2,0)内恰有两个零点当且仅当
解得0＜a＜
.
所以a的取值范围是
.
考前必练系列答案科目：高中数学 来源： 题型：
【题目】已知点
直线AM，BM相交于点M，且它们的斜率之和为2.
（1）设
且
，求
的表达式，并写出函数的定义域；
（2）判断函数的奇偶性？并给出证明;
（3）试用函数单调性的定义证明：在定义域上不是增函数，但在（0，1）∪（1，+
）上为增函数.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知数列{an}的前n项和Sn满足：Sn＝
＋
－1，且an>0，n∈N*.
（1）求a1，a2，a3，并猜想{an}的通项公式；
（2）证明（1）中的猜想.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，在多面体
中，四边形
为矩形，
，
均为等边三角形，
，
．
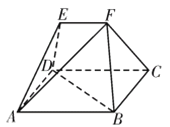
（1）过
作截面与线段
交于点
，使得
平面
，试确定点的位置，并予以证明；
（2）在（1）的条件下，求直线
与平面
所成角的正弦值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图所示，正方体ABCD－A′B′C′D′的棱长为1，E，F分别是棱AA′，CC′的中点，过直线EF的平面分别与棱BB′、DD′分别交于M，N两点，设BM＝x，x∈[0,1]，给出以下四个结论：
①平面MENF⊥平面BDD′B′；
②直线AC∥平面MENF始终成立；
③四边形MENF周长L＝f(x)，x∈[0,1]是单调函数；
④四棱锥C′－MENF的体积V＝h(x)为常数；
以上结论正确的是__________．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】下列命题：
①对立事件一定是互斥事件；②若A，B为两个随机事件，则P(A∪B)＝P(A)＋P(B)；③若事件A，B，C彼此互斥，则P(A)＋P(B)＋P(C)＝1；④若事件A，B满足P(A)＋P(B)＝1，则A与B是对立事件．
其中正确命题的个数是( )
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知f(x)＝
sinωx＋
cosωx(ω＞0)的部分图象如图所示．
(1)求ω的值；
(2)若x∈(－
，
)，求f(x)的值域；
(3)若方程3[f(x)]2－f(x)＋m＝0在x∈(－，)内有解，求实数m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
