
【题目】如图,已知圆![]() 与
与![]() 轴交于
轴交于![]() 两点(
两点(![]() 在
在![]() 的上方),直线
的上方),直线![]() .
.

(1)当![]() 时,求直线
时,求直线![]() 被圆
被圆![]() 截得的弦长;
截得的弦长;
(2)若![]() ,点
,点![]() 为直线
为直线![]() 上一动点(不在
上一动点(不在![]() 轴上),直线
轴上),直线![]() 的斜率分别为
的斜率分别为![]() ,直线
,直线![]() 与圆的另一交点分别
与圆的另一交点分别![]() .
.
①问是否存在实数![]() ,使得
,使得![]() 成立?若存在,求出
成立?若存在,求出![]() 的值;若不存在,说明理由;
的值;若不存在,说明理由;
②证明:直线![]() 经过定点,并求出定点坐标.
经过定点,并求出定点坐标.
科目:高中数学 来源: 题型:
【题目】筒车是我国古代发明的一种水利灌溉工具,因其经济又环保,至今还在农业生产中得到使用,如左下图.假定在水流量稳定的情况下,半径为3m的筒车上的每一个盛水桶都按逆时针方向作角速度为![]() rad/min的匀速圆周运动,平面示意图如右下图,己知筒车中心O到水面BC的距离为2m,初始时刻其中一个盛水筒位于点P0处,且∠P0OA=
rad/min的匀速圆周运动,平面示意图如右下图,己知筒车中心O到水面BC的距离为2m,初始时刻其中一个盛水筒位于点P0处,且∠P0OA=![]() (OA//BC),则8min后该盛水筒到水面的距离为____m.
(OA//BC),则8min后该盛水筒到水面的距离为____m.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将函数f(x)=2sin(2x﹣![]() )的图象向左平移
)的图象向左平移![]() 个单位,再向上平移1个单位,得到函数y=g(x)的图象,若y=g(x)在[0,b](b>0)上至少含有10个零点,则b的最小值为
个单位,再向上平移1个单位,得到函数y=g(x)的图象,若y=g(x)在[0,b](b>0)上至少含有10个零点,则b的最小值为
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,一个底面水平放置的倒圆锥形容器,它的轴截面是正三角形,容器内有一定量的水,水深为![]() . 若在容器内放入一个半径为 1 的铁球后,水面所在的平面恰好经过铁球的球心
. 若在容器内放入一个半径为 1 的铁球后,水面所在的平面恰好经过铁球的球心![]() (水没有溢出),则
(水没有溢出),则![]() 的值为( )
的值为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某机构为了调查某市同时符合条件![]() 与
与![]() (条件
(条件![]() :营养均衡,作息规律;条件
:营养均衡,作息规律;条件![]() :经常锻炼,劳逸结合)的高中男生的体重
:经常锻炼,劳逸结合)的高中男生的体重![]() (单位:
(单位:![]() )与身高
)与身高![]() (单位:
(单位: ![]() )是否存在较好的线性关系,该机构搜集了
)是否存在较好的线性关系,该机构搜集了![]() 位满足条件的高中男生的数据,得到如下表格:
位满足条件的高中男生的数据,得到如下表格:
身高/ |
|
|
|
|
|
|
体重/ |
|
|
|
|
|
|
根据表中数据计算得到![]() 关于
关于![]() 的线性回归方程对应的直线的斜率为
的线性回归方程对应的直线的斜率为![]() .
.
(1)求![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() (
(![]() 精确到整数部分);
精确到整数部分);
(2)已知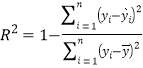 ,且当
,且当![]() 时,回归方程的拟合效果较好。试结合数据
时,回归方程的拟合效果较好。试结合数据![]() ,判断(1)中的回归方程的拟合效果是否良好?
,判断(1)中的回归方程的拟合效果是否良好?
(3)该市某高中有![]() 位男生同时符合条件
位男生同时符合条件![]() 与
与![]() ,将这
,将这![]() 位男生的身高(单位:
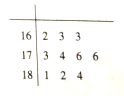
位男生的身高(单位:![]() )的数据绘制成如下的茎叶图。利用(1)中的回归方程估计这
)的数据绘制成如下的茎叶图。利用(1)中的回归方程估计这![]() 位男生的体重未超过
位男生的体重未超过![]() 的所有男生体重(单位:
的所有男生体重(单位:![]() )的平均数(结果精确到整数部分).
)的平均数(结果精确到整数部分).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高一举行了一次数学竞赛,为了了解本次竞赛学生的成绩情况,从中抽取了部分学生的分数(得分取正整数,满分为![]() )作为样本(样本容量为
)作为样本(样本容量为![]() )进行统计,按照[50,60),[60,70),[70,80),[80,90),[90,100]的分组作出频率分布直方图,已知得分在[50,60),[90,100]的频数分别为8,2.
)进行统计,按照[50,60),[60,70),[70,80),[80,90),[90,100]的分组作出频率分布直方图,已知得分在[50,60),[90,100]的频数分别为8,2.

(1)求样本容量![]() 和频率分布直方图中的
和频率分布直方图中的![]() 的值;
的值;
(2)估计本次竞赛学生成绩的中位数;
(3)在选取的样本中,从竞赛成绩在![]() 分以上(含
分以上(含![]() 分)的学生中随机抽取
分)的学生中随机抽取![]() 名学生,求所抽取的
名学生,求所抽取的![]() 名学生中至少有一人得分在
名学生中至少有一人得分在![]() 内的概率.
内的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】高二数学期中测试中,为了了解学生的考试情况,从中抽取了![]() 个学生的成绩(满分为100分)进行统计.按照[50,60), [60,70), [70,80), [80,90), [90,100]的分组作出频率分布直方图,并作出样本分数的茎叶图(图中仅列出得分在[50,60), [90,100]的数据).
个学生的成绩(满分为100分)进行统计.按照[50,60), [60,70), [70,80), [80,90), [90,100]的分组作出频率分布直方图,并作出样本分数的茎叶图(图中仅列出得分在[50,60), [90,100]的数据).

(1)求样本容量![]() 和频率分布直方图中
和频率分布直方图中![]() 的值;
的值;
(2)在选取的样本中,从成绩是80分以上(含80分)的同学中随机抽取3名参加志愿者活动,所抽取的3名同学中至少有一名成绩在[90,100]内的概率。.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() 的右顶点A(2,0),且过点
的右顶点A(2,0),且过点 ![]()
(Ⅰ)求椭圆C的方程;
(Ⅱ)过点B(1,0)且斜率为k1(k1≠0)的直线l于椭圆C相交于E,F两点,直线AE,AF分别交直线x=3于M,N两点,线段MN的中点为P,记直线PB的斜率为k2 , 求证:k1k2为定值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com