分析:(1)连结EC
1,根据平行四边形的判定与性质,证出四边形ABC
1D
1是平行四边形,从而得出AD
1∥BC
1,所以∠EBC
1为异面直线AD
1与BE所成的角.由线面垂直的判定与性质,利用勾股定理算出Rt△D
1DB中BE、EC
1的长,利用三角函数的定义加以计算,可得直线AD
1与BE所成角的正切值;
(2)由(1)的结论得BE⊥侧面DCC
1D
1,从而得到BE⊥EF.因此由线面垂直判定定理,可得若EF⊥BC
1则EF⊥平面BEC
1,得到EF⊥EC
1.进而在矩形DCC
1D
1中研究,可得当DF=
时△DEF∽△CC
1E成立,此时EF⊥EC
1.由此可得当DF=
时,EF⊥平面BEC
1成立,满足直线EF与BC
1所成的角为90°.
解答:解:(1)连结EC
1,在直四棱柱ABCD-A
1B
1C
1D
1中,
∵AB
CD,CD
C
1D
1,
∴AB
C
1D
1,可得四边形ABC
1D
1是平行四边形.
∴AD
1∥BC
1,可得∠EBC
1为异面直线AD
1与BE所成的角.
∵BD=BC=1,E为DC的中点,∴BE⊥CD,
∵直四棱柱ABCD-A
1B
1C
1D
1中,平面CC
1D
1D⊥平面ABCD,平面CC
1D
1D∩平面ABCD=CD,
∴BE⊥侧面DCC
1D
1,
∵EC
1?侧面DCC
1D
1,
∴BE⊥EC
1.
∵AB=CD=
,BD=BC=1,
∴△BCD是等腰直角三角形,
可得BE=
BC=
,
又∵在Rt△BEC
1中,EC
1=
=
,
∴tan∠EBC
1=
=3,
即直线AD
1与BE所成角的正切值等于3;
(2)∵由(1)知,BE⊥侧面DCC
1D
1,EF?侧面DCC
1D
1,
∴BE⊥EF.
又∵DE=EC=
,CC
1=AA
1=2.
∴当DF=
时,CE:DF=CC
1:DE=2
,
结合∠EDF=∠C
1CE=90°,
可得△DEF∽△CC
1E,
此时∠DEF+∠CEC
1=90°,可得∠FEC
1=90°,
即EF⊥EC
1.
又∵BE⊥EF,EB∩EC
1=E,
∴EF⊥平面BEC
1,
∵BC
1?平面BEC
1,
∴EF⊥BC
1,可得EF与BC
1所成的角等于90°.
因此当DF=
时,直线EF与BC
1所成的角为90°.
点评:本题给出特殊的直四棱柱,求异面直线所成角的正切值,并探索两条直线异面垂直的问题.着重考查直棱柱的性质、线面垂直与面面垂直的判定与性质、相似三角形的判定与性质和异面直线所成角的定义与求法等知识,属于中档题.同时考查学生的计算能力与空间想象能力,能正确作出辅助线、得到所求的空间角,是解答本题的关键.

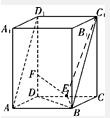
 如图,直四棱柱ABCD-A1B1C1D1的底面ABCD为平行四边形,其中AB=
如图,直四棱柱ABCD-A1B1C1D1的底面ABCD为平行四边形,其中AB=


 阅读快车系列答案
阅读快车系列答案 如图,直三棱柱ABC-A1B1C1中,AB⊥BC,D为AC的中点,AA1=AB=2.
如图,直三棱柱ABC-A1B1C1中,AB⊥BC,D为AC的中点,AA1=AB=2. 如图,直四棱柱ABCD-A1B1C1D1的底面ABCD是菱形,∠ABC=45°,其侧面展开图是边长为8的正方形.E、F分别是侧棱AA1、CC1上的动点,AE+CF=8.
如图,直四棱柱ABCD-A1B1C1D1的底面ABCD是菱形,∠ABC=45°,其侧面展开图是边长为8的正方形.E、F分别是侧棱AA1、CC1上的动点,AE+CF=8. (2012•房山区二模)如图,直四棱柱ABCD-A1B1C1D1中,底面ABCD是菱形,且∠ABC=60°,E为棱CD的中点.
(2012•房山区二模)如图,直四棱柱ABCD-A1B1C1D1中,底面ABCD是菱形,且∠ABC=60°,E为棱CD的中点.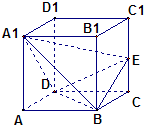 如图,在四棱柱ABC-A1B1C1D1中,AA1⊥底面ABCD,底面ABCD是菱形,∠DAB=60°,AA1=4,AB=2,点E在棱CC1上,点E是棱C1C上一点.
如图,在四棱柱ABC-A1B1C1D1中,AA1⊥底面ABCD,底面ABCD是菱形,∠DAB=60°,AA1=4,AB=2,点E在棱CC1上,点E是棱C1C上一点.