
【题目】某市为了宣传环保知识,举办了一次“环保知识知多少”的问卷调查活动(一人答一份).现从回收的年龄在![]() 岁的问卷中随机抽取了
岁的问卷中随机抽取了![]() 份, 统计结果如下面的图表所示.
份, 统计结果如下面的图表所示.
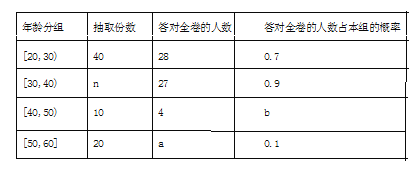
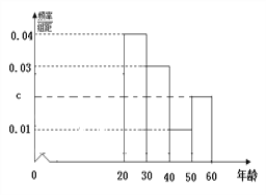
(1)分别求出![]() 的值;
的值;
(2)从年龄在![]() 答对全卷的人中随机抽取
答对全卷的人中随机抽取![]() 人授予“环保之星”,求年龄在
人授予“环保之星”,求年龄在![]() 的人中至少有
的人中至少有![]() 人被授予“环保之星”的概率.
人被授予“环保之星”的概率.
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】某公司制定了一个激励销售人员的奖励方案:当销售利润不超过20万元时,按销售利润的20%进行奖励;当销售利润超过20万元时,若超出部分为A万元,则超出部分按2log5(A+2)进行奖励,没超出部分仍按销售利润的20%进行奖励.记奖金总额为y(单位:万元),销售利润为x(单位:万元).
(1)写出该公司激励销售人员奖励方案的函数表达式;
(2)如果业务员老张获得8万元的奖励,那么他的销售利润是多少万元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】共享单车的出现方便了人们的出行,深受市民的喜爱.为调查某校大学生对共享单车的使用情况,从该校8000名学生随机抽取了100位同学进行调查,得到这100名同学每周使用共享单车的时间(单位:小时)频率分布直方图.
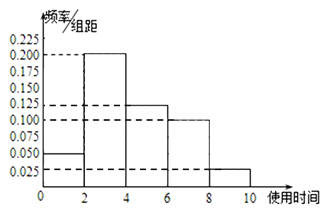
(1)已知该校大一学生有2400人,求抽取的100名学生中大一学生人数;
(2)根据频率分布直方图求该校大学生每周使用共享单车的平均时间.
(3)![]() 从抽取的100个样本中,用分层抽样的方法抽取使用共享单车时间超过6小时同学5人,再从这5人中任选2人,求这2人使用共享单车时间都不超过8小时的概率.
从抽取的100个样本中,用分层抽样的方法抽取使用共享单车时间超过6小时同学5人,再从这5人中任选2人,求这2人使用共享单车时间都不超过8小时的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有一个“乱点鸳鸯谱”节目:每次邀请四对青年夫妻,先由每人随机抽签获得顺序展示才艺,再由观众通过投票的方式实施男女配对(观众不知道他们的真实配对情况).
(Ⅰ)求正确配对家庭数的期望;
(Ⅱ)设有![]() 对夫妻,记他们完全错位的配对种类总数为
对夫妻,记他们完全错位的配对种类总数为![]() .
.
①求![]() ,
, ![]() ,
, ![]() ;
;
②推导![]() ,
, ![]() ,
, ![]() 所满足的关系式.
所满足的关系式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(Ⅰ)若关于![]() 的不等式
的不等式![]() 在
在![]() 上恒成立,求
上恒成立,求![]() 的取值范围;
的取值范围;
(Ⅱ)设函数![]() ,在(Ⅰ)的条件下,试判断
,在(Ⅰ)的条件下,试判断![]() 在
在![]() 上是否存在极值.若存在,判断极值的正负;若不存在,请说明理由.
上是否存在极值.若存在,判断极值的正负;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=kx(k≠0),且满足f(x+1)f(x)=x2+x,
(1)求函数f(x)的解析式;
(2)若函数f(x)为R上的增函数,h(x)= ![]() (f(x)≠1),问是否存在实数m使得h(x)的定义域和值域都为[m,m+1]?若存在,求出m的值,若不存在,请说明理由.
(f(x)≠1),问是否存在实数m使得h(x)的定义域和值域都为[m,m+1]?若存在,求出m的值,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某食品店为了了解气温对销售量的影响,随机记录了该店1月份中5天的日销售量![]() (单位:千克)与该地当日最低气温
(单位:千克)与该地当日最低气温![]() (单位:
(单位: ![]() )的数据,如下表:
)的数据,如下表:
| 2 | 5 | 8 | 9 | 11 |
| 12 | 10 | 8 | 8 | 7 |
(1)求出![]() 与
与![]() 的回归方程
的回归方程![]() ;
;
(2)判断![]() 与
与![]() 之间是正相关还是负相关;若该地1月份某天的最低气温为6
之间是正相关还是负相关;若该地1月份某天的最低气温为6![]() ,请用所求回归方程预测该店当日的营业额.
,请用所求回归方程预测该店当日的营业额.
附: 回归方程![]() 中,
中,  ,
,![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com