
【题目】某中学高三年级有学生500人,其中男生300人,女生200人。为了研究学生的数学成绩是否与性别有关,采用分层抽样的方法,从中抽取了100名学生,统计了他们期中考试的数学分数,然后按照性别分为男、女两组,再将两组的分数分成5组: ![]() 分别加以统计,得到如图所示的频率分布直方图。
分别加以统计,得到如图所示的频率分布直方图。

(I)从样本分数小于110分的学生中随机抽取2人,求两人恰为一男一女的概率;
(II)若规定分数不小于130分的学生为“数学尖子生”,请你根据已知条件完成2×2列联表,并判断是否有90%的把握认为“数学尖子生与性别有关”?
 附表:
附表:
【答案】(Ⅰ)P=![]() ;(Ⅱ)见解析.
;(Ⅱ)见解析.
【解析】试题分析:(1)根据分层抽样原理计算抽取的男、女生人数,利用列举法计算基本事件数,求出对应的概率值;
(2)由频率分布直方图计算对应的数据,填写列联表,计算![]() 值,对照数表即可得出概率结论.
值,对照数表即可得出概率结论.
试题解析:(Ⅰ)由已知得,抽取的100名学生中,男生60名,女生40名,
分数小于等于110分的学生中,男生人有60×0.05=3(人),记为A1,A2,A3;
女生有40×0.05=2(人),记为B1,B2; ………………2分
从中随机抽取2名学生,所有的可能结果共有10种,它们是:
(A1,A2),(A1,A3),(A2,A3),(A1,B1),(A1,B2),
(A2,B1),(A2,B2),(A3,B1),(A3,B2),(B1,B2);
其中,两名学生恰好为一男一女的可能结果共有6种,它们是:
(A1,B1),(A1,B2),(A2,B1),
(A2,B2),(A3,B1),(A3,B2);
故所求的概率为P=![]() .
.
(Ⅱ)由频率分布直方图可知,
在抽取的100名学生中,男生 60×0.25=15(人),女生40×0.375=15(人); …7分
据此可得2×2列联表如下:
数学尖子生 | 非数学尖子生 | 合计 | |
男生 | 15 | 45 | 60 |
女生 | 15 | 25 | 40 |
合计 | 30 | 70 | 100 |
(9分)
所以得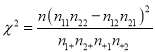
![]() ;
;
因为1.79<2.706,
所以没有90%的把握认为“数学尖子生与性别有关”


科目:高中数学 来源: 题型:
【题目】某高校在2014年的自主招生考试成绩中随机抽取100名学生的笔试成绩,按成绩分组,得到的频率分布表如下表所示.
组号 | 分组 | 频数 | 频率 |
第1组 | [160,165) | 5 | 0.050 |
第2组 | [165,170) | n | 0.350 |
第3组 | [170,175) | 30 | p |
第4组 | [175,180) | 20 | 0.200 |
第5组 | [180,185] | 10 | 0.100 |
合计 | 100 | 1.000 |

(1)求频率分布表中n,p的值,并补充完整相应的频率分布直方图;
(2)为了能选拔出最优秀的学生,高校决定在笔试成绩高的第3、4、5组中用分层抽样的方法抽取6名学生进入第二轮面试,则第3、4、5组每组各抽取多少名学生进入第二轮面试?
(3)在(2)的前提下,学校决定从6名学生中随机抽取2名学生接受甲考官的面试,求第4组至少有1名学生被甲考官面试的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=3ax2+2bx+c,且有a+b+c=0,f(0)>0,f(1)>0.
(Ⅰ)求证:a>0,且﹣2< ![]() <﹣1;
<﹣1;
(Ⅱ)求证:函数y=f(x)在区间(0,1)内有两个不同的零点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,O为坐标原点,A、B、C三点满足 ![]() =
= ![]()
![]() +
+ ![]()
![]() .
.
(1)求证:A、B、C三点共线;
(2)已知A(1,cosx),B(1+cosx,cosx)(0≤x≤ ![]() ),f(x)=
),f(x)= ![]()
![]() ﹣(2m+
﹣(2m+ ![]() )|
)| ![]() |的最小值为﹣
|的最小值为﹣ ![]() ,求实数m的值.
,求实数m的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】20名同学参加某次数学考试成绩(单位:分)的频率分布直方图如下:

(Ⅰ)求频率分布直方图中![]() 的值;
的值;
(Ⅱ)分别求出成绩落在![]() ,
, ![]() 中的学生人数;
中的学生人数;
(Ⅲ)从成绩在![]() 的学生中任选2人,求此2人的成绩都在
的学生中任选2人,求此2人的成绩都在![]() 中的概率.
中的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】福利彩票“双色球”中红球的号码可以从01,02,03,…,32,33这33个二位号码中选取,小明利用如图所示的随机数表选取红色球的6个号码,选取方法是从第1行第9列和第10列的数字开始从左到右依次选取两个数字,则第四个被选中的红色球号码为( )
81 47 23 68 63 93 17 90 12 69 86 81 62 93 50 60 91 33 75 85 61 39 85 |
06 32 35 92 46 22 54 10 02 78 49 82 18 86 70 48 05 46 88 15 19 20 49 |
A. 12 B. 33 C. 06 D. 16
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P﹣ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC=2,E是PC的中点,作EF⊥PB交PB于点F. 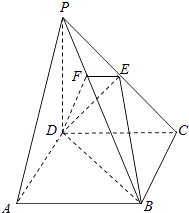
(1)证明:PA∥平面EDB;
(2)证明:PB⊥平面EFD.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某住宅小区的平面图呈圆心角为120°的扇形AOB,小区的两个出入口设置在点A及点C处,且小区里有一条平行于BO的小路CD,已知某人从C沿CD走到D用了10分钟,从D沿DA走到A用了6分钟,若此人步行的速度为每分钟50米,求该扇形的半径OA的长(精确到1米) 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com