
【题目】如图,在四棱锥P﹣ABCD中,底面ABCD是菱形,且∠ABC=120°.点E是棱PC的中点,平面ABE与棱PD交于点F. (Ⅰ)求证:AB∥EF;
(Ⅱ)若PA=PD=AD=2,且平面PAD⊥平面ABCD,求平面PAF与平面AEF所成的二面角的正弦值.
【答案】证明:(Ⅰ)∵底面ABCD是菱形,∴AB∥CD, 又∵AB面PCD,CD面PCD,∴AB∥面PCD
又∵A,B,E,F四点共面,且平面ABEF∩平面PCD=EF,
∴AB∥EF
解:(Ⅱ)取AD中点G,连接PG,GB,
∵PA=PD,∴PG⊥AD,
又∵平面PAD⊥平面ABCD,且平面PAD∩平面ABCD=AD,
∴PG⊥平面ABCD
∴PG⊥GB,在菱形ABCD中,∵AB=AD,∠DAB=60°,G是AD中点,∴AD⊥GB,
如图,以G为原点,GA、GB、GP所在直线为坐标轴建立空间直角坐标系G﹣xyz
由PA=PD=AD=2得,G(0,0,0),A(1,0,0),![]() ,
, ![]() ,D(﹣1,0,0),
,D(﹣1,0,0),
又∵AB∥EF,点E是棱PC中点,∴点F是棱PD中点,
∴  ,
, 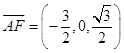 ,
, ![]() ,
,
设平面AFE的法向量为 ![]() ,
,
则有  ,∴
,∴  ,
,
不妨令x=3,则平面AFE的一个法向量为 ![]() ,
,
∵BG⊥平面PAD,∴ ![]() 是平面PAF的一个法向量,
是平面PAF的一个法向量,  ,
,
∴平面PAF与平面AFE所成的二面角的正弦值为:![]() .
. 
【解析】(Ⅰ)推导出AB∥CD,从而AB∥面PCD,由此能证明AB∥EF.(Ⅱ)取AD中点G,连接PG,GB,以G为原点,GA、GB、GP所在直线为坐标轴建立空间直角坐标系G﹣xyz,利用向量法能求出平面PAF与平面AFE所成的二面角的正弦值.
【考点精析】本题主要考查了空间中直线与直线之间的位置关系的相关知识点,需要掌握相交直线:同一平面内,有且只有一个公共点;平行直线:同一平面内,没有公共点;异面直线: 不同在任何一个平面内,没有公共点才能正确解答此题.


科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2sinxsin(x+3φ)是奇函数,其中φ∈(0, ![]() ),则函数g(x)=cos(2x﹣φ)的图象( )
),则函数g(x)=cos(2x﹣φ)的图象( )
A.关于点( ![]() ,0)对称
,0)对称
B.可由函数f(x)的图象向右平移 ![]() 个单位得到
个单位得到
C.可由函数f(x)的图象向左平移 ![]() 个单位得到
个单位得到
D.可由函数f(x)的图象向左平移 ![]() 个单位得到
个单位得到
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若关于x的不等式|3x+2|+|3x﹣1|﹣t≥0的解集为R,记实数t的最大值为a.
(1)求a;
(2)若正实数m,n满足4m+5n=a,求 ![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=a(x+ ![]() )+blnx(其中a,b∈R)
)+blnx(其中a,b∈R)
(Ⅰ)当b=﹣4时,若f(x)在其定义域内为单调函数,求a的取值范围;
(Ⅱ)当a=﹣1时,是否存在实数b,使得当x∈[e,e2]时,不等式f(x)>0恒成立,如果存在,求b的取值范围,如果不存在,说明理由(其中e是自然对数的底数,e=2.71828…).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】抛物线y2=2px(p>0)的焦点为F,准线为l,A,B是抛物线上的两个动点,且满足∠AFB= ![]() .设线段AB的中点M在l上的投影为N,则
.设线段AB的中点M在l上的投影为N,则 ![]() 的最大值是( )
的最大值是( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() 的一个焦点为F(3,0),其左顶点A在圆O:x2+y2=12上.
的一个焦点为F(3,0),其左顶点A在圆O:x2+y2=12上.
(1)求椭圆C的方程;
(2)直线l:x=my+3(m≠0)交椭圆C于M,N两点,设点N关于x轴的对称点为N1(点N1与点M不重合),且直线N1M与x轴的交于点P,试问△PMN的面积是否存在最大值?若存在,求出这个最大值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系 ![]() 中,已知椭圆
中,已知椭圆 ![]() 的离心率为
的离心率为 ![]() ,C为椭圆上位于第一象限内的一点.
,C为椭圆上位于第一象限内的一点.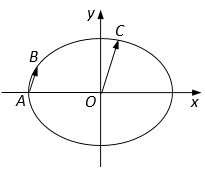
(1)若点 ![]() 的坐标为
的坐标为 ![]() ,求a,b的值;
,求a,b的值;
(2)设A为椭圆的左顶点,B为椭圆上一点,且 ![]() ,求直线AB的斜率.
,求直线AB的斜率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】△ABC的内角A,B,C的对边分别为a,b,c,已知a(sinA﹣sinB)=(c﹣b)(sinC+sinB) (Ⅰ)求角C;
(Ⅱ)若c= ![]() ,△ABC的面积为
,△ABC的面积为 ![]() ,求△ABC的周长.
,求△ABC的周长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com