【题目】△ABC中，角A，B，C的对边分别为a，b，c，且2bcosC+c=2a．
（Ⅰ）求角B的大小；
（Ⅱ）若
，求
的值．
【答案】（1）
（2）
【解析】试题分析：（1）由于2bcosC+c=2a，是关于边的一次齐次式，所以用正弦定理把边化为角，可得到
，
。（2）由（1）中和
，可知A，B角己知，同时根据三角形内角为
，也可以sinC,所以
，可解。
试题解析：（Ⅰ）在△ABC中，∵2bcosC+c=2a，
由正弦定理，得2sinBcosC+sinC=2sinA，
∵A+B+C=π，
∴sinA=sin（B+C）=sinBcosC+cosBsinC，…
∴2sinBcosC+sinC=2（sinBcosC+cosBsinC），
∴sinC=2cosBsinC，
∵0＜C＜π，∴sinC≠0，
∴，
∵0＜B＜π，∴．
（Ⅱ）∵三角形ABC中，
，
∴
，
∴
，
∴
科目：高中数学 来源： 题型：
【题目】某蔬果经销商销售某种蔬果，售价为每公斤25元，成本为每公斤15元.销售宗旨是当天进货当天销售.如果当天卖不出去，未售出的全部降价以每公斤10元处理完.根据以往的销售情况，得到如图所示的频率分布直方图：
（1）根据频率分布直方图计算该种蔬果日需求量的平均数
（同一组中的数据用该组区间中点值代表）；
（2）该经销商某天购进了250公斤这种蔬果，假设当天的需求量为
公斤
，利润为
元.求关于的函数关系式，并结合频率分布直方图估计利润不小于1750元的概率.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，
的三条内线段
、
、
交于点
、用红、蓝两种颜色对的三条边线和三条内线段染色，使同色的三线不交于一点.证明：在图中所有的三角形中，至少存在两个同色三角形，且它的各边或延长线被另一线截得的两线段之比的和大于3.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在平面直角坐标系
中，已知椭圆
的左、右焦点分别为
，且点与椭圆C的上顶点构成边长为2的等边三角形.
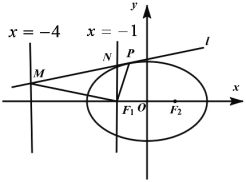
（1）求椭圆C的方程；
（2）已知直线l与椭圆C相切于点P，且分别与直线
和直线
相交于点
.试判断
是否为定值，并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
