
分析 (Ⅰ)运用等差数列的通项公式与求和公式,根据条件列方程,求出首项和公差,得到通项an,运用n=1时,b1=T1,n>1时,bn=Tn-Tn-1,求出bn;
(Ⅱ)写出cn,然后运用分组求和,一组为等差数列,一组为等比数列,分别应用求和公式化简即可.
解答 解:(Ⅰ)设等差数列{an}的公差为d,
由题意,得$\left\{\begin{array}{l}{{a}_{1}+d=8}\\{4{a}_{1}+6d=40}\end{array}\right.$,
解得a1=d=4,
∴an=4n,
∵Tn-2bn+3=0,∴当n=1时,b1=3,当n≥2时,Tn-1-2bn-1+3=0,
两式相减,得bn=2bn-1,(n≥2)
则数列{bn}为等比数列,
∴bn=3•2n-1;
(Ⅱ)cn=$\left\{\begin{array}{l}{4n,n为奇数}\\{3•{2}^{n-1},n为偶数}\end{array}\right.$.
当n为偶数时,P2n=(a1+a3+…+a2n-1)+(b2+b4+…+b2n)
=(4+12+…+8n-4)+(6+24+…+3•22n-1)
=4n+$\frac{1}{2}$n(n-1)•8+$\frac{6(1-{4}^{n})}{1-4}$
=22n+1+4n2-2.
点评 本题主要考查等差数列和等比数列的通项与求和公式的运用,考查方程的思想在数列中的运用,同时考查数列的通项与前n项和的关系式,考查数列的求和方法:分组求和,是一道综合题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
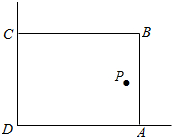 在美化校园的活动中,某兴趣小组想借助如图所示的直角墙角(两墙足够长),用16m长的篱笆围成一个矩形花园ABCD(篱笆只围AB、BC两边),在P处有一棵树与墙CD、AD的距离分别是a(0<a<12)m和4m,现需要将这棵树围在花园内(含边界,不考虑树的粗细).设矩形ABCD的面积是ym2,长DA为xm.
在美化校园的活动中,某兴趣小组想借助如图所示的直角墙角(两墙足够长),用16m长的篱笆围成一个矩形花园ABCD(篱笆只围AB、BC两边),在P处有一棵树与墙CD、AD的距离分别是a(0<a<12)m和4m,现需要将这棵树围在花园内(含边界,不考虑树的粗细).设矩形ABCD的面积是ym2,长DA为xm.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com