
已知函数 的图象过点(2,0).
的图象过点(2,0).
⑴求m的值;
⑵证明 的奇偶性;
的奇偶性;
⑶判断 在
在 上的单调性,并给予证明;
上的单调性,并给予证明;
(1)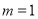 ;(2)
;(2)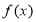 是奇函数;(3)
是奇函数;(3)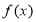 在
在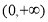 上为单调增函数.
上为单调增函数.
【解析】
试题分析:(1)由已知可将点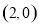 代入函数
代入函数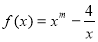 ,得
,得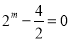 ,从而求出
,从而求出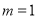 ;(2)根据函数奇偶性的定义可证明(定义法证明函数的奇偶性的步骤:①先判断定义域是否关于原点对称;②再判断
;(2)根据函数奇偶性的定义可证明(定义法证明函数的奇偶性的步骤:①先判断定义域是否关于原点对称;②再判断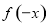 与
与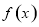 的关系,即若
的关系,即若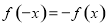 则为奇函数,若
则为奇函数,若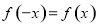 则为偶函数).由(1)得函数
则为偶函数).由(1)得函数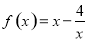 ,其定义为
,其定义为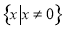 关于原点对称,又
关于原点对称,又 ,所以函数
,所以函数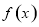 为奇函数;(3)根据函数单调性的定义可判断(定义法判断函数的单调性一般步骤为:①在其定义域内任取两个自变量
为奇函数;(3)根据函数单调性的定义可判断(定义法判断函数的单调性一般步骤为:①在其定义域内任取两个自变量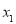 、
、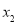 ,且
,且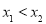 ;②作差(或作商)比较
;②作差(或作商)比较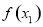 与
与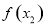 的大小;③得出结论,即若
的大小;③得出结论,即若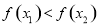 则为单调递增函数,若
则为单调递增函数,若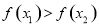 则为单调递减函数).
则为单调递减函数).
试题解析:⑴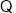
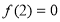 ,∴
,∴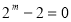 ,
,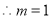 . 2分
. 2分
⑵因为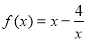 ,定义域为
,定义域为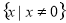 ,关于原点成对称区间. 3分
,关于原点成对称区间. 3分
又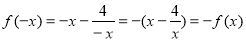 ,
,
所以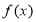 是奇函数. 6分
是奇函数. 6分
⑶设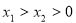 ,则
,则
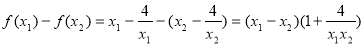 8分
8分
因为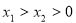 ,所以
,所以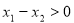 ,
,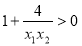 ,
,
所以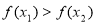 ,因此,
,因此,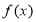 在
在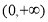 上为单调增函数. 10分
上为单调增函数. 10分
考点:函数的解析式、奇偶性、单调性


 智能训练练测考系列答案
智能训练练测考系列答案科目:高中数学 来源:2016届辽宁大连教育学院高一第一学期期末考试数学试卷(解析版) 题型:解答题
如图,已知 是圆的直径,
是圆的直径, 垂直圆所在的平面,
垂直圆所在的平面, 是圆上任一点,
是圆上任一点, 是线段
是线段 的中点,
的中点, 是线段
是线段 上的一点.
上的一点.
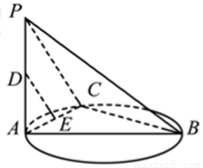
求证:(Ⅰ)若 为线段
为线段 中点,则
中点,则 ∥平面
∥平面 ;
;
(Ⅱ)无论 在
在 何处,都有
何处,都有 .
.
查看答案和解析>>
科目:高中数学 来源:2016届贵州省黔东南州高一上学期期末考试数学试卷(解析版) 题型:解答题
(本小题满分12分)某医药研究所开发的一种新药,如果成年人按规定的剂量服用,据监测:服药后每毫升血液中的含药量 (单位:微克)与时间
(单位:微克)与时间 (单位:小时)之间近似满足如图所示的曲线.
(单位:小时)之间近似满足如图所示的曲线.

(Ⅰ)写出第一次服药后 与
与 之间的函数关系式
之间的函数关系式 ;
;
(Ⅱ)据进一步测定:每毫升血液中含药量不少于 微克时,治疗有效.问:服药多少小时开始有治疗效果?治疗效果能持续多少小时?(精确到0.1)(参考数据:
微克时,治疗有效.问:服药多少小时开始有治疗效果?治疗效果能持续多少小时?(精确到0.1)(参考数据: ).
).
查看答案和解析>>
科目:高中数学 来源:2016届福建省高一上学期期中考试数学试卷(解析版) 题型:填空题
设全集U=R,A={x| x<-2,或x≥1},B={x| a-1<x<a+1},B ∁RA,则实数a的取值范围是______.
∁RA,则实数a的取值范围是______.
查看答案和解析>>
科目:高中数学 来源:2016届福建省高一上学期期中考试数学试卷(解析版) 题型:选择题
右图是函数 的图像,它与x轴有4个不同的公共点.给出下列四个区间,不能用二分法求出函数
的图像,它与x轴有4个不同的公共点.给出下列四个区间,不能用二分法求出函数 在区间( )上的零点.
在区间( )上的零点.

A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源:2016届福建省宁德市高一上学期期末考试数学试卷(解析版) 题型:选择题
设函数 ,用二分法求方程
,用二分法求方程 的近似根过程中,计算得到
的近似根过程中,计算得到 ,则方程的根落在区间
,则方程的根落在区间
A. B.
B.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源:2016届福建三明A片区高中联盟校高一上期末数学试卷(解析版) 题型:选择题
已知函数 。若
。若 ,则
,则 的值( )
的值( )
A.一定是 B.一定是
B.一定是
C.是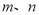 中较大的数 D.是
中较大的数 D.是 中较小的数
中较小的数
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com