试题分析:利用矩阵特征值
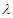
及其对应特征向量
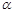
性质:
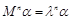
进行化简.先根据矩阵M的特征多项式求出其特征值

,进而求出对应的特征向量
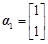
,
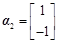
.再将

分解成特征向量,即
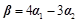
,最后利用性质求结果,即
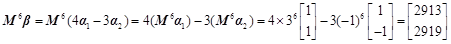
试题解析:解:矩阵M的特征多项式为

.
令
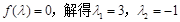
,对应的一个特征向量分别为
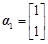
,
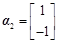
. 5分
令
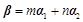
,得

.

.10分
练习册系列答案
相关习题
科目:高中数学
来源:不详
题型:解答题
已知矩阵
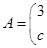
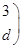
,若矩阵
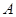
属于特征值6的一个特征向量为
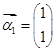
,属于特征值1的一个特征向量
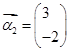
.
(1)求矩阵
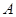
的逆矩阵;
(2)计算
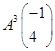
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
已知线性变换
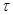
:
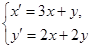
对应的矩阵为
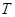
,向量β
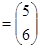
.
(Ⅰ)求矩阵
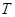
的逆矩阵
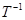
;
(Ⅱ)若向量α在
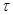
作用下变为向量β,求向量α.
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
在直角坐标平面内,将每个点绕原点按逆时针方向旋转

的变换

所对应的矩阵为

,将每个点横、纵坐标分别变为原来的

倍的变换

所对应的矩阵为

.
(1)求矩阵

的逆矩阵

;
(2)求曲线

先在变换

作用下,然后在变换

作用下得到的曲线方程.
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
已知矩阵
M=

,若矩阵
M的逆矩阵
M-1=

,求a、b的值.
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
求直线x+y=5在矩阵
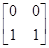
对应的变换作用下得到的图形.
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
对任意实数x,矩阵
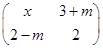
总存在特征向量,求m的取值范围.
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
已知M=
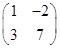
.
(1)求逆矩阵M
-1.
(2)若向量X满足MX=
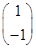
,试求向量X.
查看答案和解析>>

 ,
, ,计算
,计算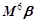 .
. 的变换
的变换 所对应的矩阵为
所对应的矩阵为 ,将每个点横、纵坐标分别变为原来的
,将每个点横、纵坐标分别变为原来的 倍的变换
倍的变换 所对应的矩阵为
所对应的矩阵为 .
. 的逆矩阵
的逆矩阵 ;
; 先在变换
先在变换 作用下,然后在变换
作用下,然后在变换 作用下得到的曲线方程.
作用下得到的曲线方程.