
【题目】已知函数y=f(x+1)定义域是[﹣2,3],则y=f(2x﹣1)的定义域( )
A.![]()
B.[﹣1,4]
C.[﹣5,5]
D.[﹣3,7]
【答案】A
【解析】解:解:∵函数y=f(x+1)定义域为[﹣2,3],∴x∈[﹣2,3],则x+1∈[﹣1,4],
即函数f(x)的定义域为[﹣1,4],
再由﹣1≤2x﹣1≤4,得:0≤x≤ ![]() ,
,
∴函数y=f(2x﹣1)的定义域为[0, ![]() ].
].
故选A.
【考点精析】关于本题考查的函数的定义域及其求法,需要了解求函数的定义域时,一般遵循以下原则:①![]() 是整式时,定义域是全体实数;②
是整式时,定义域是全体实数;②![]() 是分式函数时,定义域是使分母不为零的一切实数;③
是分式函数时,定义域是使分母不为零的一切实数;③![]() 是偶次根式时,定义域是使被开方式为非负值时的实数的集合;④对数函数的真数大于零,当对数或指数函数的底数中含变量时,底数须大于零且不等于1,零(负)指数幂的底数不能为零才能得出正确答案.
是偶次根式时,定义域是使被开方式为非负值时的实数的集合;④对数函数的真数大于零,当对数或指数函数的底数中含变量时,底数须大于零且不等于1,零(负)指数幂的底数不能为零才能得出正确答案.


科目:高中数学 来源: 题型:
【题目】如图,四棱锥S﹣ABCD中,底面ABCD是边长为4的菱形,∠ABC=60°,SA⊥平面ABCD,且SA=4,M在棱SA上,且AM=1,N在棱SD上且SN=2ND. (Ⅰ)求证:CN∥面BDM;
(Ⅱ)求直线SD与平面BDM所成的角的正弦值.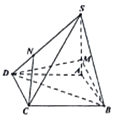
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数y=f(x)在区间I上是增函数,且函数 ![]() 在区间I上是减函数,则称函数f(x)是区间I上的“H函数”.对于命题:①函数
在区间I上是减函数,则称函数f(x)是区间I上的“H函数”.对于命题:①函数 ![]() 是(0,1)上的“H函数”;②函数
是(0,1)上的“H函数”;②函数 ![]() 是(0,1)上的“H函数”.下列判断正确的是( )
是(0,1)上的“H函数”.下列判断正确的是( )
A.①和②均为真命题
B.①为真命题,②为假命题
C.①为假命题,②为真命题
D.①和②均为假命题
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)=lg(1﹣x2),集合A={x|y=f(x)},B={y|y=f(x)},则如图中阴影部分表示的集合为( ) 
A.[﹣1,0]
B.(﹣1,0)
C.(﹣∞,﹣1)∪[0,1)
D.(﹣∞,﹣1]∪(0,1)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数y=f(x),若在定义域内存在x0 , 使得f(﹣x0)=﹣f(x0)成立,则称x0为函数f(x)的局部对称点.
(I)若a∈R且a≠0,求函数f(x)=ax2+x﹣a的“局部对称点”;
(II)若函数f(x)=4x﹣m2x+1+m2﹣3在R上有局部对称点,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)的定义域是(0,+∞),f'(x)为f(x)的导函数,且满足f(x)<f'(x),则不等式 ![]() f(2)的解集是( )
f(2)的解集是( )
A.(﹣∞,2)∪(1,+∞)
B.(﹣2,1)
C.(﹣∞,﹣1)∪(2,+∞)
D.(﹣1,2)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x+ex﹣a , g(x)=ln(x+2)﹣4ea﹣x , 其中e为自然对数的底数,若存在实数x0 , 使f(x0)﹣g(x0)=3成立,则实数a的值为( )
A.﹣ln2﹣1
B.﹣1+ln2
C.﹣ln2
D.ln2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com