练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知f(x)=(x≠a).

    (1)若a=-2,试证f(x)在(-∞,-2)上单调递增.

    (2)若a>0且f(x)在(1,+∞)上单调递减,求a的取值范围.

     

    (1)见解析 (2) (0,1]

    【解析】(1)任设x1<x2<-2, (0,1]

    则f(x1)-f(x2)=-=.

    ∵(x1+2)(x2+2)>0,x1-x2<0,

    ∴f(x1)<f(x2),

    ∴f(x)在(-∞,-2)上单调递增.

    (2)任设1<x1<x2,则

    f(x1)-f(x2)=-

    =.

    ∵a>0,x2-x1>0,

    ∴要使f(x1)-f(x2)>0,只需(x1-a)(x2-a)>0恒成立,∴a≤1.

    综上所述知a的取值范围是(0,1].

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：2014年高考数学文二轮专题复习与测试选修4-1几何证明选讲练习卷（解析版） 题型：解答题

    如图，圆O的半径OC垂直于直径AB，弦CD交半径 OA于E，过D的切线与BA的延长线交于M.

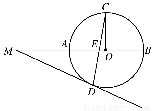
    (1)求证：MD＝ME；

    (2)设圆O的半径为1，MD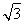＝，求MA及CE的长．

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学全程总复习课时提升作业（六）第二章第三节练习卷（解析版） 题型：填空题

    已知奇函数f(x)满足f(x+2)=-f(x),且当x∈(0,1)时,f(x)=2x,则f()的值为　　　　.

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学全程总复习课时提升作业（八）第二章第五节练习卷（解析版） 题型：选择题

    计算:lg-lg+lg7=　　　　.

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学全程总复习课时提升作业（八）第二章第五节练习卷（解析版） 题型：选择题

    若点(a,b)在y=lgx的图象上,a≠1,则下列点也在此图象上的是(　　)

    (A)(,b) (B)(10a,1-b)

    (C)(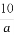,b+1) (D)(a2,2b)

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学全程总复习课时提升作业（五）第二章第二节练习卷（解析版） 题型：选择题

    已知函数f(x)是定义在(0,+∞)上的单调函数,若对任意x∈(0,+∞),都有f(f(x)-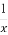)=2,则f()的值是(　　)

    (A)5 (B)6 (C)7 (D)8

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学全程总复习课时提升作业（五）第二章第二节练习卷（解析版） 题型：选择题

    函数f(x)=1-(　　)

    (A)在(-1,+∞)上单调递增

    (B)在(1,+∞)上单调递增

    (C)在(-1,+∞)上单调递减

    (D)在(1,+∞)上单调递减

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学全程总复习课时提升作业（二）第一章第二节练习卷（解析版） 题型：选择题

    下面四个条件中,使a>b成立的充分而不必要条件是(　　)

    (A)a>b+1 (B)a>b-1 (C)a2>b2 (D)a3>b3

     

    查看答案和解析>>

    科目：高中数学 来源：2014年高考数学全程总复习课时提升作业（七）第二章第四节练习卷（解析版） 题型：选择题

    若函数f(x)=a|2x-4|(a>0,a≠1)满足f(1)=,则f(x)的单调递减区间是(　　)

    (A)(-∞,2] (B)[2,+∞)

    (C)[-2,+∞) (D)(-∞,-2]

     

    查看答案和解析>>

    同步练习册答案