已知函数f(x)=loga(x+1)(a>1),若函数y=g(x)的图象与函数y=f(x)的图象关于原点对称.
(1)写出函数g(x)的解析式;
(2)求不等式2f(x)+g(x)≥0的解集A;
(3)问是否存在m∈R*,使不等式f(x)+2g(x)≥logam的解集恰好是A?若存在,请求出m的值;若不存在,请说明理由.
【答案】
分析:(1)、设P(x,y)为y=g(x)图象上任意一点,则P关于原点的对称点Q(-x,-y)在y=f(x)的图象上,把Q(-x,-y)代入函数y=log
a(x+1)(a>1),就能得到函数g(x)的解析式.
(2)、不等式2f(x)+g(x)≥0等价于

,求出
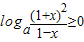
的解集即得到集合A.
(3)、先假设存在m∈R
*使命题成立,则由f(x)+2g(x)≥log
am,得log
a(1+x)≥log
a[m(1-x)
2],然后根据不等式1+x≥m(1-x)
2的解集与集合A的关系求出m的值.
解答:解:(1)设P(x,y)为y=g(x)图象上任意一点,
则P关于原点的对称点Q(-x,-y)在y=f(x)的图象上,
所以-y=log
a(-x+1),即g(x)=-log
a(1-x);
(2)由
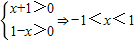
,原不等式可化为

,
∵a>1,∴

,且-1<x<1⇒0≤x<1即A=[0,1).
(3)假设存在m∈R
*使命题成立,则由f(x)+2g(x)≥log
am,
得log
a(1+x)≥log
a[m(1-x)
2]
∵a>1,∴不等式组

的解集恰为A=[0,1),
只需不等式1+x≥m(1-x)
2,即mx
2-(2m+1)x+m-1≤0的解集为A=[0,b),且b≥1,
易得m=1即为所求,故存在实数m=1使命题成立.
点评:本题是对数函数的综合题,难度较大.在解题是要注意对称性质的灵活应用和等价命题的合理转化.

 ,求出
,求出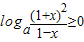 的解集即得到集合A.
的解集即得到集合A.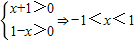 ,原不等式可化为
,原不等式可化为 ,
, ,且-1<x<1⇒0≤x<1即A=[0,1).
,且-1<x<1⇒0≤x<1即A=[0,1). 的解集恰为A=[0,1),
的解集恰为A=[0,1),
