
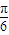 ��|��һ��x��R���������
��|��һ��x��R���������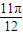 ��=0�� ��|f��
��=0�� ��|f�� ��|��|f��
��|��|f��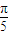 ��|��
��|��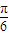 ��k��+
��k��+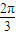 ]��k��Z����
]��k��Z����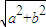 sin��2x+�ȣ��������֪����ʽ��f��
sin��2x+�ȣ��������֪����ʽ��f�� ���Ǻ�����������Сֵ���Ӷ��õ�
���Ǻ�����������Сֵ���Ӷ��õ� sin��2x+
sin��2x+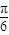 +k�У�=±
+k�У�=± sin��2x+
sin��2x+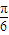 �����ٸ������Ǻ���y=Asin����x+�գ���ͼ�������ʣ��Ը�ѡ����������жϣ��ɵâ٢ۢ�ͨ��֤���ɵ�����ȷ�ԣ����ڢܴ��ڷ���˵�����Dz���ȷ��
�����ٸ������Ǻ���y=Asin����x+�գ���ͼ�������ʣ��Ը�ѡ����������жϣ��ɵâ٢ۢ�ͨ��֤���ɵ�����ȷ�ԣ����ڢܴ��ڷ���˵�����Dz���ȷ�� sin��2x+�ȣ������нǦ�����cos��=
sin��2x+�ȣ������нǦ�����cos��=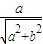 ��sin��=
��sin��=
 ��|��һ��x��R�������
��|��һ��x��R������� ��=
��= ��-
��- ����2×
����2×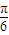 +��=
+��= +k��k��Z
+k��k��Z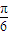 +k��k��Z��f��x��=
+k��k��Z��f��x��= sin��2x+
sin��2x+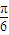 +k��=
+k��= sin��2x+
sin��2x+ ����-
����- sin��2x+
sin��2x+ ��
�� +
+ ��=sin2��=0������f��
��=sin2��=0������f��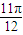 ��=±
��=± sin��2×
sin��2× +
+ ��=0���ʢ���ȷ��
��=0���ʢ���ȷ�� ��|=|
��|=| sin��2×
sin��2× +
+ ��|=
��|=

 ��|=|
��|=|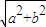 sin��2×
sin��2×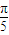 +
+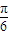 ��|=
��|=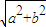 sin
sin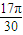 ��
��

 ��|��|f��
��|��|f�� ��|���ʢڲ���ȷ��
��|���ʢڲ���ȷ��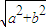 sin��2x+
sin��2x+ ����-
����- sin��2x+
sin��2x+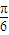 ����
����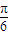 ��k��+
��k��+ ]��k��Z����һ���������䣬�ʢܲ���ȷ��
]��k��Z����һ���������䣬�ʢܲ���ȷ��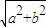 ��ƽ����b2��a2+b2ì�ܣ��ʼ��費����
��ƽ����b2��a2+b2ì�ܣ��ʼ��費����


| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
| 1 | f(-2-an) |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
| 1 |
| f(-2-an) |
| 1 |
| an+1 |
| 1 |
| an+2 |
| 1 |
| a2n |
| 12 |
| 35 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
| 3x-1 |
| x+1 |
| 1 |
| 2 |
| t-1 |
| t |
| s+1 |
| s |
| s+1 |
| s |
| t-1 |
| t |
| 11 |
| 17 |
| 1 |
| xn-1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2011-2012ѧ��㶫ʡ����һ�и߶����ϣ�������ѧ�Ծ����Ŀƣ��������棩 ���ͣ������
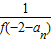 ��n��N*��
��n��N*���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2011-2012ѧ��㶫ʡ����һ�и߶����ϣ�������ѧ�Ծ������ƣ��������棩 ���ͣ������
 ��
��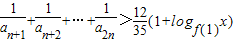 �Բ�С��2�����������������x��ȡֵ��Χ��
�Բ�С��2�����������������x��ȡֵ��Χ���鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com