
【题目】如图,在棱长为3的正方体ABCD-A1B1C1D1中,A1E=CF=1.
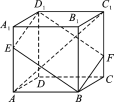
(1)求两条异面直线AC1与BE所成角的余弦值;
(2)求直线BB1与平面BED1F所成角的正弦值.
【答案】(1)![]() .(2)
.(2)![]() .
.
【解析】
(1)先根据题意建立空间直角坐标系,求得向量![]() 和向量
和向量![]() 的坐标,再利用线线角的向量方法求解.
的坐标,再利用线线角的向量方法求解.
(2)先求得平面BED1F的一个法向量,易知向量![]() 的坐标,再利用线面角的向量方法求解.
的坐标,再利用线面角的向量方法求解.
(1)以D为原点,建立空间直角坐标系Dxyz,如图所示,
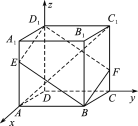
则A(3,0,0),C1(0,3,3),![]() =(-3,3,3),
=(-3,3,3),
B(3,3,0),E(3,0,2),![]() =(0,-3,2).
=(0,-3,2).
所以cos〈![]() 〉=
〉=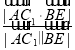 =
=![]() =
=![]() ,
,
故两条异面直线AC1与BE所成角的余弦值为![]() .
.
(2) B(3,3,0),![]() =(0,-3,2),
=(0,-3,2),![]() =(3,0,-1).
=(3,0,-1).
设平面BED1F的一个法向量为n=(x,y,z),
由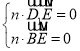 得
得![]()
所以![]() 则n=(x,2x,3x),不妨取n=(1,2,3),
则n=(x,2x,3x),不妨取n=(1,2,3),
设直线BB1与平面BED1F所成的角为α,则
sinα=|cos〈![]() ,n〉|=
,n〉|=![]() =
=![]() .
.
所以直线BB1与平面BED1F所成角的正弦值为![]() .
.


 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案科目:高中数学 来源: 题型:
【题目】由国家统计局提供的数据可知,2012年至2018年中国居民人均可支配收入![]() (单位:万元)的数据如下表:
(单位:万元)的数据如下表:
年份 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 |
年份代号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
人均可支配收入 | 1.65 | 1.83 | 2.01 | 2.19 | 2.38 | 2.59 | 2.82 |
(1)求![]() 关于
关于![]() 的线性回归方程(系数精确到0.01);
的线性回归方程(系数精确到0.01);
(2)利用(1)中的回归方程,分析2012年至2018年中国居民人均可支配收入的变化情况,并预测2019年中国居民人均可支配收入.
附注:参考数据:![]() ,
,![]() .
.
参考公式:回归直线方程![]() 的斜率和截距的最小二乘估计公式分别为:
的斜率和截距的最小二乘估计公式分别为: 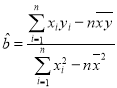 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知正方体![]() ,过对角线
,过对角线![]() 作平面
作平面![]() 交棱
交棱![]() 于点E,交棱
于点E,交棱![]() 于点F,则:
于点F,则:
①平面![]() 分正方体所得两部分的体积相等;
分正方体所得两部分的体积相等;
②四边形![]() 一定是平行四边形;
一定是平行四边形;
③平面![]() 与平面
与平面![]() 不可能垂直;
不可能垂直;
④四边形![]() 的面积有最大值.
的面积有最大值.
其中所有正确结论的序号为( )
A.①④B.②③C.①②④D.①②③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥PABCD中,PA⊥底面ABCD,AD∥BC,AB=AC=AD=3,PA=BC=4.
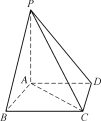
(1)求异面直线PB与CD所成角的余弦值;
(2)求平面PAD与平面PBC所成锐二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱ABCA1B1C1中,AB⊥AC,AB=2,AC=4,AA1=2,![]() =λ
=λ![]() .
.
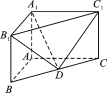
(1)若λ=1,求直线DB1与平面A1C1D所成角的正弦值;
(2)若二面角B1- A1C1-D的大小为60°,求实数λ的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 为坐标原点,椭圆
为坐标原点,椭圆![]() :
:![]() 的焦距为
的焦距为![]() ,直线
,直线![]() 截圆
截圆![]() :
:![]() 与椭圆
与椭圆![]() 所得的弦长之比为
所得的弦长之比为![]() ,椭圆
,椭圆![]() 与
与![]() 轴正半轴的交点分别为
轴正半轴的交点分别为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设点![]() (
(![]() 且
且![]() )为椭圆
)为椭圆![]() 上一点,点
上一点,点![]() 关于
关于![]() 轴的对称点为
轴的对称点为![]() ,直线
,直线![]() ,
,![]() 分别交
分别交![]() 轴于点
轴于点![]() ,
,![]() .试判断
.试判断![]() 是否为定值?若是求出该定值,若不是定值,请说明理由.
是否为定值?若是求出该定值,若不是定值,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,椭圆
中,椭圆![]() 过点
过点![]() ,焦点
,焦点![]() ,圆
,圆![]() 的直径为
的直径为![]() .
.
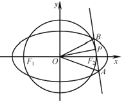
(1)求椭圆![]() 及圆
及圆![]() 的方程;
的方程;
(2)设直线![]() 与圆
与圆![]() 相切于第一象限内的点
相切于第一象限内的点![]() ,直线
,直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点.若
两点.若![]() 的面积为
的面积为![]() ,求直线
,求直线![]() 的方程.
的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com