
【题目】已知椭圆![]() :
: ![]() 经过点
经过点 ,左右焦点分别为
,左右焦点分别为![]() 、
、![]() ,圆
,圆![]() 与直线
与直线![]() 相交所得弦长为2.
相交所得弦长为2.
(Ⅰ)求椭圆![]() 的标准方程;
的标准方程;
(Ⅱ)设![]() 是椭圆
是椭圆![]() 上不在
上不在![]() 轴上的一个动点,
轴上的一个动点, ![]() 为坐标原点,过点
为坐标原点,过点![]() 作
作![]() 的平行线交椭圆
的平行线交椭圆![]() 于
于![]() 、
、![]() 两个不同的点,求
两个不同的点,求![]() 的取值范围.
的取值范围.
 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案科目:高中数学 来源: 题型:
【题目】【2015高考山东文数】某中学调查了某班全部![]() 名同学参加书法社团和演讲社团的情况,数据如下表:(单位:人)
名同学参加书法社团和演讲社团的情况,数据如下表:(单位:人)
参加书法社团 | 未参加书法社团 | |
参加演讲社团 |
|
|
未参加演讲社团 |
|
|
(1)从该班随机选![]() 名同学,求该同学至少参加上述一个社团的概率;
名同学,求该同学至少参加上述一个社团的概率;
(2)在既参加书法社团又参加演讲社团的![]() 名同学中,有5名男同学
名同学中,有5名男同学![]()
![]() 名女同学
名女同学![]() 现从这
现从这![]() 名男同学和
名男同学和![]() 名女同学中各随机选
名女同学中各随机选![]() 人,求
人,求![]() 被选中且
被选中且![]() 未被选中的概率.
未被选中的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】来自某校一班和二班的共计9名学生志愿服务者被随机平均分配到运送矿泉水、清扫卫生、维持秩序这三个岗位服务,且运送矿泉水岗位至少有一名一班志愿者的概率是![]() .
.
(Ⅰ)求清扫卫生岗位恰好一班1人、二班2人的概率;
(Ⅱ)设随机变量![]() 为在维持秩序岗位服务的一班的志愿者的人数,求
为在维持秩序岗位服务的一班的志愿者的人数,求![]() 分布列及期望.
分布列及期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】质监部门从某超市销售的甲、乙两种食用油中分别各随机抽取100桶检测某项质量指标,由检测结果得到如下的频率分布直方图:
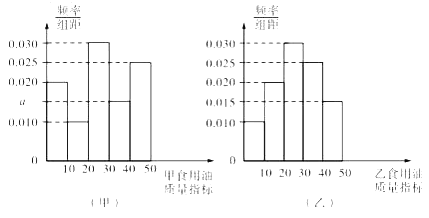
(Ⅰ)写出频率分布直方图(甲)中![]() 的值;记甲、乙两种食用油100桶样本的质量指标的方差分别为
的值;记甲、乙两种食用油100桶样本的质量指标的方差分别为![]() ,
,![]() ,试比较
,试比较![]() ,
,![]() 的大小(只要求写出答案);
的大小(只要求写出答案);
(Ⅱ)估计在甲、乙两种食用油中随机抽取1捅,恰有一桶的质量指标大于20;
(Ⅲ)由频率分布直方图可以认为,乙种食用油的质量指标值![]() 服从正态分布
服从正态分布![]() .其中
.其中![]() 近似为样本平均数
近似为样本平均数![]() ,
,![]() 近似为样本方差
近似为样本方差![]() ,设
,设![]() 表示从乙种食用油中随机抽取10桶,其质量指标值位于(14.55,38.45)的桶数,求
表示从乙种食用油中随机抽取10桶,其质量指标值位于(14.55,38.45)的桶数,求![]() 的数学期望.
的数学期望.
注:①同一组数据用该区问的中点值作代表,计算得![]()
②若![]()
![]() ,则
,则![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在某地区某高传染性病毒流行期间,为了建立指标显示疫情已受控制,以便向该地区居众显示可以过正常生活,有公共卫生专家建议的指标是“连续7天每天新增感染人数不超过5人”,根据连续7天的新增病倒数计算,下列各选项中,一定符合上述指标的是( )
①平均数 ![]() ;
;
②标准差S≤2;
③平均数 ![]() 且标准差S≤2;
且标准差S≤2;
④平均数 ![]() 且极差小于或等于2;
且极差小于或等于2;
⑤众数等于1且极差小于或等于1.
A.①②
B.③④
C.③④⑤
D.④⑤
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知命题p:不等式(m-1)x2+(m-1)x+2>0的解集是R,命题q:sin x+cos x>m.如果对于任意的x∈R,命题p是真命题且命题q为假命题,求m的范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)是奇函数,并且在R上为增函数,若0≤θ≤ ![]() 时,f(msinθ)+f(1﹣m)>0恒成立,则实数m的取值范围是( )
时,f(msinθ)+f(1﹣m)>0恒成立,则实数m的取值范围是( )
A.(0,1)
B.(﹣∞,0)
C.(﹣∞,1)
D.(﹣∞, ![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com