
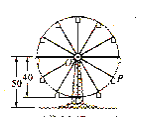
【题目】如图所示,摩天轮的半径为![]() 米,点
米,点![]() 距地面高度为
距地面高度为![]() 米,摩天轮做匀速运动,每
米,摩天轮做匀速运动,每![]() 分钟转一圈,以点
分钟转一圈,以点![]() 为原点,过点
为原点,过点![]() 且平行与地平线的直线为
且平行与地平线的直线为![]() 轴建立平面直角坐标系
轴建立平面直角坐标系![]() ,设点
,设点![]() 的起始位置在最低点(且在最低点开始时),设在时刻
的起始位置在最低点(且在最低点开始时),设在时刻![]() (分钟)时点
(分钟)时点![]() 距地面的高度
距地面的高度![]() (米),则
(米),则![]() 与
与![]() 的函数关系式
的函数关系式
![]()
![]() __________.在摩天轮旋转一周内,点
__________.在摩天轮旋转一周内,点![]() 到地面的距离不小于
到地面的距离不小于![]() 米的时间长度为 __________(分钟)
米的时间长度为 __________(分钟)
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:高中数学 来源: 题型:
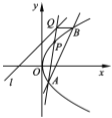
【题目】已知直线![]() 的方程为
的方程为![]() ,点
,点![]() 是抛物线
是抛物线![]() 上到直线
上到直线![]() 距离最小的点,点
距离最小的点,点![]() 是抛物线上异于点
是抛物线上异于点![]() 的点,直线
的点,直线![]() 与直线
与直线![]() 交于点
交于点![]() ,过点
,过点![]() 与
与![]() 轴平行的直线与抛物线
轴平行的直线与抛物线![]() 交于点
交于点![]() .
.
(Ⅰ)求点![]() 的坐标;
的坐标;
(Ⅱ)证明直线![]() 恒过定点,并求这个定点的坐标.
恒过定点,并求这个定点的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】集成电路E由3个不同的电子元件组成,现由于元件老化,3个电子元件能正常工作的概率分别降为![]() ,
,![]() ,
,![]() ,且每个电子元件能否正常工作相互独立。若3个电子元件中至少有2个正常工作,则E能正常工作,否则就需要维修,且维修集成电路E所需要费用为100元。
,且每个电子元件能否正常工作相互独立。若3个电子元件中至少有2个正常工作,则E能正常工作,否则就需要维修,且维修集成电路E所需要费用为100元。
(Ⅰ)求集成电路E需要维修的概率;
(Ⅱ)若某电子设备共由2个集成电路E组成,设X为该电子设备需要维修集成电路所需费用。求X的分布列和均值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解某地区某种农产品的年产量![]() (单位:吨)对价格
(单位:吨)对价格![]() (单位:千元/吨)和利润
(单位:千元/吨)和利润![]() 的影响,对近五年该农产品的年产量和价格统计如下表:
的影响,对近五年该农产品的年产量和价格统计如下表:

(1)求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)若每吨该农产品的成本为2千元,假设该农产品可全部卖出,预测当年产量为多少时,年利润![]() 取到最大值?(结果保留两位小数)
取到最大值?(结果保留两位小数)
参考公式: 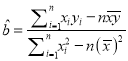 ,
, ![]()
参考数据: ![]() ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
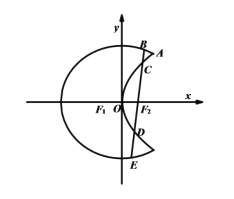
【题目】如图“月亮图”是由曲线![]() 与
与![]() 构成,曲线
构成,曲线![]() 是以原点
是以原点![]() 为中点,
为中点, ![]() 为焦点的椭圆的一部分,曲线
为焦点的椭圆的一部分,曲线![]() 是以
是以![]() 为顶点,
为顶点, ![]() 为焦点的抛物线的一部分,
为焦点的抛物线的一部分, ![]() 是两条曲线的一个交点.
是两条曲线的一个交点.
(Ⅰ)求曲线![]() 和
和![]() 的方程;
的方程;
(Ⅱ)过![]() 作一条与
作一条与![]() 轴不垂直的直线,分别与曲线
轴不垂直的直线,分别与曲线![]() 依次交于
依次交于![]() 四点,若
四点,若![]() 为
为![]() 的中点,
的中点, ![]() 为
为![]() 的中点,问:
的中点,问: ![]() 是否为定值?若是求出该定值;若不是说明理由.
是否为定值?若是求出该定值;若不是说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com