
已知函数 在[1,+∞)上为增函数,且
在[1,+∞)上为增函数,且 ,
, ,
,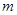 ∈R.
∈R.
(1)求θ的值;
(2)若 在[1,+∞)上为单调函数,求m的取值范围;
在[1,+∞)上为单调函数,求m的取值范围;
(3)设 ,若在[1,e]上至少存在一个
,若在[1,e]上至少存在一个 ,使得
,使得 成立,
成立,
求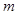 的取值范围.
的取值范围.
(1)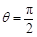 .(2)
.(2)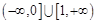 .(3)
.(3)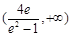
【解析】(1)解本小题关键是把题目条件转化为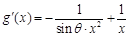 ≥0在
≥0在 上恒成立,即
上恒成立,即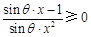 恒成立问题来解决.
恒成立问题来解决.
(2)由(1),得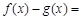
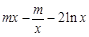 .
. .
.
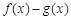 在其定义域内为单调函数,然后解题的关键就转化为
在其定义域内为单调函数,然后解题的关键就转化为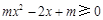 或者
或者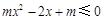 在[1,+∞)恒成立,下面可以考虑变量与参数分离求解.
在[1,+∞)恒成立,下面可以考虑变量与参数分离求解.
(3)构造函数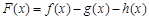 ,
, 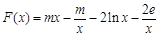
本小题就转化为F(X)的最大值大于零即可
(1)由题意,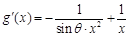 ≥0在
≥0在 上恒成立,即
上恒成立,即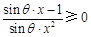 .
.
∵θ∈(0,π),∴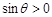 .故
.故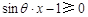 在
在 上恒成立,
上恒成立,
只须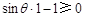 ,即
,即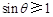 ,只有
,只有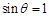 .结合θ∈(0,π),得
.结合θ∈(0,π),得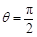 .
.
(2)由(1),得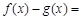
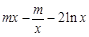 .
. .
.
∵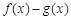 在其定义域内为单调函数,
在其定义域内为单调函数,
∴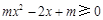 或者
或者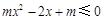 在[1,+∞)恒成立.
在[1,+∞)恒成立.
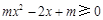 等价于
等价于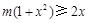 ,即
,即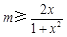 ,
,
而 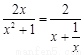 ,(
,(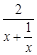 )max=1,∴
)max=1,∴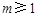 .
.
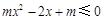 等价于
等价于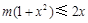 ,即
,即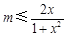 在[1,+∞)恒成立,
在[1,+∞)恒成立,
而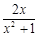 ∈(0,1],
∈(0,1],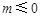 .综上,m的取值范围是
.综上,m的取值范围是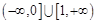 .
.
(3)构造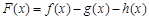 ,
,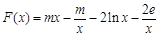 .
.
当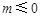 时,
时,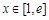 ,
,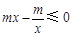 ,
,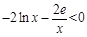 ,所以在[1,e]上不存在一个
,所以在[1,e]上不存在一个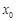 使得
使得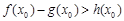 成立.
当
成立.
当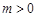 时,
时,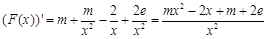 .
.
因为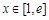 ,所以
,所以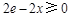 ,
,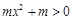 ,所以
,所以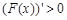 在
在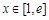 恒成立.
恒成立.
故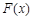 在
在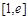 上单调递增,
上单调递增,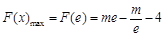 ,只要
,只要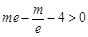 ,
,
解得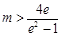 故
故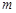 的取值范围是
的取值范围是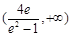


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:2011-2012学年浙江省高三上学期期中理科数学试卷 题型:解答题
已知函数 在[1,+∞)上为增函数,且
在[1,+∞)上为增函数,且 ,
, ,
, ∈R.
∈R.
(1)求θ的值;
(2)若 在[1,+∞)上为单调函数,求m的取值范围;
在[1,+∞)上为单调函数,求m的取值范围;
(3)设 ,若在[1,e]上至少存在一个
,若在[1,e]上至少存在一个 ,使得
,使得 成立,求
成立,求 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年浙江省杭州市求是高复高三11月月考文科数学 题型:解答题
(本题满分15分)
已知函数 在[1,+∞)上为增函数,且
在[1,+∞)上为增函数,且 ,
,
(1)求 的值;
的值;
(2)若 在[1,+∞)上为单调函数,求实数
在[1,+∞)上为单调函数,求实数 的取值范围;
的取值范围;
(3)若在 上至少存在一个
上至少存在一个 ,使得
,使得 成立,求实数
成立,求实数 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com