
2013年9月20日是第25个全国爱牙日。某区卫生部门成立了调查小组,调查 “常吃零食与患龋齿的关系”,对该区六年级800名学生进行检查,按患龋齿和不患龋齿分类,得汇总数据:不常吃零食且不患龋齿的学生有60名,常吃零食但不患龋齿的学生有100名,不常吃零食但患龋齿的学生有140名.
(1)能否在犯错概率不超过0.001的前提下,认为该区学生的常吃零食与患龋齿有关系?
(2)4名区卫生部门的工作人员随机分成两组,每组2人,一组负责数据收集,另一组负责数据处理.求工作人员甲分到负责收集数据组,工作人员乙分到负责数据处理组的概率.
| 0.010 | 0.005 | 0.001 |
| 6.635 | 7.879 | 10.828 |
附: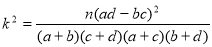
(1)学生常吃零食与患龋齿有关系(2)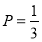
【解析】
试题分析:(1)根据题意建立相应的列联表,根据公式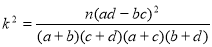 计算
计算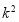 ,查表比较大小即可判断是否有关
,查表比较大小即可判断是否有关
(2)古典概型,对四名工作人员编号,利用树状图或者表格的方式列出四选两个的所有基本事件,求出符合“工作人员甲分到负责收集数据组,工作人员乙分到负责数据处理组”的基本事件数,根据古典概型概率的计算公式即可得到相应的概率.
试题解析:(1)由题意可得列联表:
| 不常吃零食 | 常吃零食 | 总计 |
不患龋齿 | 60 | 100 | 160 |
患龋齿 | 140 | 500 | 640 |
总计 | 200 | 600 | 800 |
因为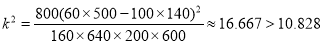 。
。
所以能在犯错率不超过0.001的前提下,为该区学生常吃零食与患龋齿有关系。
(2)设其他工作人员为丙和丁,4人分组的所有情况如下表
小组 | 1 | 2 | 3 | 4 | 5 | 6 |
收集数据 | 甲乙 | 甲丙 | 甲丁 | 乙丙 | 乙丁 | 丙丁 |
处理数据 | 丙丁 | 乙丁 | 乙丙 | 甲丁 | 甲丙 | 甲乙 |
分组的情况总有6中,工作人员甲负责收集数据且工作人员乙负责处理数据占两种,
所以工作人员甲负责收集数据且工作人员处理数据的概率是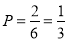 。
。
考点:古典概型 独立性检验


科目:高中数学 来源:2013-2014学年河北省唐山市高三年级第三次模拟考试理科数学试卷(解析版) 题型:解答题
在斜三棱柱 中,平面
中,平面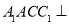 平面ABC,
平面ABC,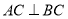 ,
,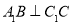 ,
,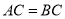 .
.
(1)求证: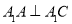 ;
;
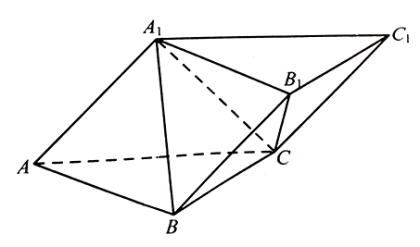
(2)若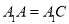 ,求二面角
,求二面角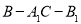 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年河北省高三下学期调研考试理科数学试卷(解析版) 题型:选择题
右面是“二分法”解方程的流程图.在①~④处应填写的内容分别是( )
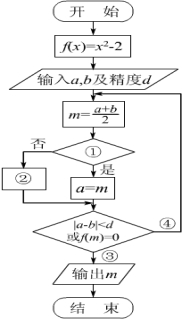
A.f(a)f(m)<0;a=m;是;否
B.f(b)f(m)<0;b=m;是;否
C.f(b)f(m)<0;m=b;是;否
D.f(b)f(m)<0;b=m;否;是
查看答案和解析>>
科目:高中数学 来源:2013-2014学年河北省高三下学期调研考试理科数学试卷(解析版) 题型:选择题
已知复数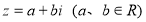 ,
,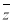 是
是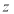 的共轭复数,且
的共轭复数,且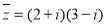 则a、b的值分别为( )
则a、b的值分别为( )
A.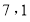 B.
B.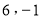 C.
C.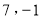 D.
D.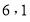
查看答案和解析>>
科目:高中数学 来源:2013-2014学年河北省高三下学期调研考试文科数学试卷(解析版) 题型:填空题
如图是甲、乙两名篮球运动员2013年赛季每场比赛得分的茎叶图,则甲、乙两人比赛得分的中位数之和为 .

查看答案和解析>>
科目:高中数学 来源:2013-2014学年河北省高三下学期调研考试文科数学试卷(解析版) 题型:选择题
某四棱锥的底面为正方形,其三视图如图所示,则该四棱锥的体积等于( )

A.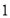 B.
B.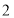 C.
C.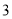 D.
D.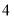
查看答案和解析>>
科目:高中数学 来源:2013-2014学年江西省鹰潭市高三第二次模拟考试理科数学试卷(解析版) 题型:解答题
为喜迎马年新春佳节,某商场在正月初六进行抽奖促销活动,当日在该店消费满500元的顾客可参加抽奖.抽奖箱中有大小完全相同的4个小球,分别标有 “马”“上”“有”“钱”.顾客从中任意取出1个球,记下上面的字后放回箱中,再从中任取1个球,重复以上操作,最多取4次,并规定若取出“钱”字球,则停止取球.获奖规则如下:依次取到标有“马”“上”“有”“钱”字的球为一等奖;不分顺序取到标有“马”“上”“有”“钱”字的球,为二等奖;取到的4个球中有标有“马”“上”“有”三个字的球为三等奖.
(1)求分别获得一、二、三等奖的概率;
(2)设摸球次数为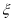 ,求
,求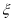 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com