
| A. | (1,5) | B. | (1,7) | C. | ($\sqrt{7}$,7) | D. | ($\sqrt{7}$,5) |
分析 把三棱锥A-BCD放置于一个长方体中,由长方体棱长和面对角线的关系推出m<5,再由∠BAC为锐角得到
32+m2-42>0,由此推得m$>\sqrt{7}$.
解答  解:将三棱锥A-BCD放置于一个长方体中,
解:将三棱锥A-BCD放置于一个长方体中,
如图:
设长方体过一个顶点的三条棱长分别为a,b,c,
则$\left\{\begin{array}{l}{{a}^{2}+{b}^{2}=9}\\{{b}^{2}+{c}^{2}=16}\\{{a}^{2}+{c}^{2}={m}^{2}}\end{array}\right.$,
∴a2+c2+2b2=25,
则m2=a2+c2<a2+c2+2b2=25,∴m<5;
∵△BNC为△BAC的射影,且∠BNC=90°,∴∠BAC为锐角.
则32+m2-42>0,即$m>\sqrt{{4}^{2}-{3}^{2}}=\sqrt{7}$.
∴m的取值范围是($\sqrt{7}$,5).
故选:D.
点评 本题考查棱锥的结构特征,考查了学生的空间想象能力和思维能力,体现了数学转化思想方法,是中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
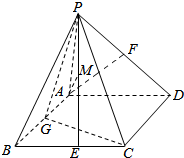 已知在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为菱形,∠ABC=60°,AB=PA=2,G、E、F分别为AB、BC、PD的中点
已知在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为菱形,∠ABC=60°,AB=PA=2,G、E、F分别为AB、BC、PD的中点查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图所示,正方体ABCD-A1B1C1D1的棱长为a,点P是棱AD上一点,且AP=$\frac{a}{3}$,过点B1,D1,P的平面交底面ABCD于PQ,Q在直线CD上,则PQ=$\frac{\sqrt{2}a}{3}$.
如图所示,正方体ABCD-A1B1C1D1的棱长为a,点P是棱AD上一点,且AP=$\frac{a}{3}$,过点B1,D1,P的平面交底面ABCD于PQ,Q在直线CD上,则PQ=$\frac{\sqrt{2}a}{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com