
【题目】已知椭圆![]() 过点
过点![]() 且椭圆的短轴长为
且椭圆的短轴长为![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)已知动直线![]() 过右焦点
过右焦点![]() ,且与椭圆
,且与椭圆![]() 分别交于
分别交于![]() 两点.试问
两点.试问![]() 轴上是否存在定点
轴上是否存在定点![]() ,使得,
,使得,![]() 恒成立?若存在求出点
恒成立?若存在求出点![]() 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
【答案】(Ⅰ)![]() (Ⅱ)存在,
(Ⅱ)存在,![]()
【解析】
(Ⅰ)由椭圆性质可知![]() ,点代入即可求得结果.
,点代入即可求得结果.
(Ⅱ)假设存在定点![]() 符合题意,①当直线
符合题意,①当直线![]() 的斜率不存在时,由
的斜率不存在时,由![]() 解得
解得![]() 或
或![]() ;②当直线
;②当直线![]() 的斜率为0时,解得
的斜率为0时,解得![]() 或
或![]() .由①②可得
.由①②可得![]() ,然后证明当
,然后证明当![]() 时,通过方程联立,借助韦达定理,坐标表示
时,通过方程联立,借助韦达定理,坐标表示![]() 即可证得结论.
即可证得结论.
解:(Ⅰ)因为椭圆![]() 过点
过点![]() ,所以
,所以![]() .
.
又椭圆的短轴长为![]() ,所以
,所以![]() ,所以
,所以![]() ,
,
解得![]() .
.
所以椭圆![]() 的方程为
的方程为![]() .
.
(Ⅱ)假设在![]() 轴上存在定点
轴上存在定点![]() ,使得
,使得![]() ,
,
①当直线![]() 的斜率不存在时,则
的斜率不存在时,则![]() ,
,![]() ,
,
![]() ,
,
由![]() ,解得
,解得![]() 或
或![]() ;
;
②当直线![]() 的斜率为0时,则
的斜率为0时,则![]() ,
,![]() ,
,![]() ,
,
由![]() ,解得
,解得![]() 或
或![]() .
.
由①②可得![]() ,即点
,即点![]() 的坐标为
的坐标为![]() .
.
下面证明当![]() 时,
时,![]() 恒成立,当直线
恒成立,当直线![]() 的斜率不存在或斜率为0时,由①②知结论成立.
的斜率不存在或斜率为0时,由①②知结论成立.
当直线斜率存在且不为0时,设其方程为![]() ,
,![]() ,
,![]() ,
,
由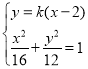 ,得
,得![]() ,
,
直线经过椭圆内一点,一定与椭圆有两个交点,
且![]() ,
,![]() .
.
![]() ,
,
所以![]()
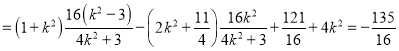 .
.
综上所述,在![]() 轴上存在定点
轴上存在定点![]() ,使得
,使得![]() 恒成立..
恒成立..


 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 和点D(2,0),直线
和点D(2,0),直线 ![]() 与抛物线C交于不同两点A、B,直线BD与抛物线C交于另一点E.给出以下判断:
与抛物线C交于不同两点A、B,直线BD与抛物线C交于另一点E.给出以下判断:
①直线OB与直线OE的斜率乘积为-2; ②![]() 轴; ③以BE为直径的圆与抛物线准线相切;
轴; ③以BE为直径的圆与抛物线准线相切;
其中,所有正确判断的序号是( )
A.①②③B.①②C.①③D.②③
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某厂接受了一项加工业务,加工出来的产品(单位:件)按标准分为A,B,C,D四个等级.加工业务约定:对于A级品、B级品、C级品,厂家每件分别收取加工费90元,50元,20元;对于D级品,厂家每件要赔偿原料损失费50元.该厂有甲、乙两个分厂可承接加工业务.甲分厂加工成本费为25元/件,乙分厂加工成本费为20元/件.厂家为决定由哪个分厂承接加工业务,在两个分厂各试加工了100件这种产品,并统计了这些产品的等级,整理如下:
甲分厂产品等级的频数分布表
等级 | A | B | C | D |
频数 | 40 | 20 | 20 | 20 |
乙分厂产品等级的频数分布表
等级 | A | B | C | D |
频数 | 28 | 17 | 34 | 21 |
(1)分别估计甲、乙两分厂加工出来的一件产品为A级品的概率;
(2)分别求甲、乙两分厂加工出来的100件产品的平均利润,以平均利润为依据,厂家应选哪个分厂承接加工业务?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C1:![]() (a>b>0)的右焦点F与抛物线C2的焦点重合,C1的中心与C2的顶点重合.过F且与x轴垂直的直线交C1于A,B两点,交C2于C,D两点,且|CD|=
(a>b>0)的右焦点F与抛物线C2的焦点重合,C1的中心与C2的顶点重合.过F且与x轴垂直的直线交C1于A,B两点,交C2于C,D两点,且|CD|=![]() |AB|.
|AB|.
(1)求C1的离心率;
(2)设M是C1与C2的公共点,若|MF|=5,求C1与C2的标准方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,直线l的参数方程为 为参数
为参数![]() ,以坐标原点O为极点,以x轴正半轴为极轴的极坐标系中,曲线C的极坐标方程为
,以坐标原点O为极点,以x轴正半轴为极轴的极坐标系中,曲线C的极坐标方程为![]() .
.
![]() 求直线l的普通方程及曲线C的直角坐标方程;
求直线l的普通方程及曲线C的直角坐标方程;
![]() 若直线l与曲线C交于A,B两点,求线段AB的中点P到坐标原点O的距离.
若直线l与曲线C交于A,B两点,求线段AB的中点P到坐标原点O的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(理)某学校高一年级学生某次身体素质体能测试的原始成绩采用百分制,已知所有这些学生的原始成绩均分布在![]() 内,发布成绩使用等级制各等级划分标准见下表,规定:
内,发布成绩使用等级制各等级划分标准见下表,规定:![]() 三级为合格等级,
三级为合格等级,![]() 为不合格等级.
为不合格等级.
百分制 | 85分及以上 | 70分到84分 | 60分到69分 | 60分以下 |
等级 |
|
|
|
|
为了解该校高一年级学生身体素质情况,从中抽取了![]() 名学生的原始成绩作为样本进行统计,按照
名学生的原始成绩作为样本进行统计,按照![]() 的分组作出频率分布直方图如图所示,样本中分数在80分及以上的所有数据的茎叶图如图所示.,
的分组作出频率分布直方图如图所示,样本中分数在80分及以上的所有数据的茎叶图如图所示.,
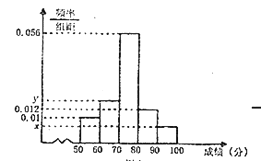
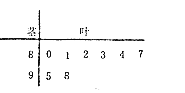
(1)求![]() 和频率分布直方图中的
和频率分布直方图中的![]() 的值;
的值;
(2)根据样本估计总体的思想,以事件发生的频率作为相应事件发生的概率,若在该校高一学生任选3人,求至少有1人成绩是合格等级的概率;
(3)在选取的样本中,从![]() 两个等级的学生中随机抽取了3名学生进行调研,记
两个等级的学生中随机抽取了3名学生进行调研,记![]() 表示所抽取的
表示所抽取的![]() 名学生中为
名学生中为![]() 等级的学生人数,求随机变量
等级的学生人数,求随机变量![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某国营企业集团公司现有员工1000名,平均每人每年创造利润10万元.为了激化内部活力,增强企业竞争力,集团公司董事会决定优化产业结构,调整出![]() (
(![]() )名员工从事第三产业;调整后,他们平均每人每年创造利润
)名员工从事第三产业;调整后,他们平均每人每年创造利润![]() 万元
万元![]() ,剩下的员工平均每人每年创造的利润可以提高
,剩下的员工平均每人每年创造的利润可以提高![]() %.
%.
(Ⅰ)若要保证剩余员工创造的年总利润不低于原来1000名员工创造的年总利润,则最多调整出多少名员工从事第三产业?
(Ⅱ)在(1)的条件下,若调整出的员工创造的年总利润始终不高于剩余员工创造的年总利润,则实数![]() 的取值范围是多少?
的取值范围是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com